Acknowledgements
Praveen, Joey, Raghu, Hamid and Cliff acknowledge the contributions of John McPherson, Guy Lohman, Beau Shekita, Dave Simmen, Lori Strain, Monica Urata, and Surendra Verma at IBM Almaden, Navin Kabra and Jignesh Patel at University of Wisconsin, and Inderpal Mumick for the original magic rewriting code. Divesh, Peter and Sudarshan would like to thank Brian Hart for discussions that lead them to start thinking of how Constraint Magic rewriting might be implemented using generalizations of semijoins, Bill McKenna for discussions regarding costbased algebraic optimizers and feedback on the paper, and Tim Griffin for discussions about bag operators.
Praveen Seshadri was supported by an IBM Graduate Student Fellowship. Raghu Ramakrishnan was supported by a David and Lucile Packard Foundation Fellowship in Science and Engineering, a Presidential Young Investigator Award, with matching grants from Digital Equipment Corporation, Tandem and Xerox, and NSF grant IRI9011563. Joseph Hellerstein was supported by NSF grant IRI9157357.
Алгебра ?-полусоединений
В своей реализации мы использовали перезапись на основе магических множеств путем ее «встраивания» («piggybacking») в существующие механизмы оптимизатора. Если бы система основывалась на алгебраическом, управляемом правилами оптимизаторе, таком как Volcano [GM93], был бы возможен и подход к расширению алгебры запросов для моделирования магических множеств. В этом разделе мы представляем такое алгебраическое расширение, помогающее охарактеризовать точное пространство возможных вариантов. Алгебраические эквивалентности приводят к преобразованию запросов, которые могут применяться в оценочном стиле, возможно, с использованием уже представленных методов оценки, или с использованием тщательного исследования пространства поиска.
Альтернативы перезаписи
В приведенном перезаписанном запросе фильтрующее множество содержит все большие отделы, в которых работают молодые сотрудники. Это фильтрующее множество является наиболее ограничительным из всех возможных. Можно использовать менее ограничительное фильтрующее множество. Фильтрующее множество может содержать все большие отделы или все отделы с молодыми сотрудниками. В каждом из этих случаев перезаписанные запросы будут отличаться от запроса, представленного на рис. 2, но они будут иметь похожую общую структуру и будут производить одни и те же результаты. В то время как эти варианты могут приводить к большему числу вычислений внутри представления, они могут быть дешевле в целом (поскольку будут более дешево вычисляться таблицы PartialResult или Filter). В общем случае имеется много способов создания фильтрующего множества, каждый из которых соответствует некоторому подмножеству множества таблиц, указанных в разделе FROM табличного выражения представления PartialResult. Если все отделы являются большими и включают молодых служащих, перезаписанные запросы не обеспечат никаких преимуществ перед исходным запросом, и их выполнение может даже оказаться более дорогостоящим. Наконец, если имеется несколько атрибутов соединения, то требуется принять решение о том, все ли атрибуты соединения будут вносить вклад в фильтрующее множество, или же будут использоваться только некоторые атрибуты. Однако в подавляющем большинстве запросов имеется в точности один атрибут соединения, так что обычно этот аспект не является важным.
Конкретная комбинация результатов выбора по отношению к вычислению фильтрующего множества называется «стратегией сторонней передачи информации» («sideways information passing strategy, SIPS), названный так по той причине, что фильтрующее множество передает атрибуты соединения в определение представления «сторонним образом». Одна из SIPS приводит к наилучшему плану выполнения запроса. Однако это зависит от таблиц и предикатов, участвующих в запросе, и характеристик среды выполнения.
В настоящее время отсутствует какое- либо практическое решение для выбора SIPS в оценочном стиле. Вместо этого, существующие системы, выполняющие перезапись на основе магических множеств, придерживаются одного из двух подходов:
Использовать перезапись на основе магических множеств с SIPS по умолчанию (обычно «слева-направо» и разрешать пользователю указывать другие SIPS или блокировать перезапись на основе магических множеств. Этот подход используется в CORAL [RSSS94]. Одновременно оптимизировать запрос с перезаписью на основе магических множеств и без нее и выбирать самый дешевый план. Для перезаписи на основе магических множеств выбирать SIPS на основе некоторой эвристики. Этот подход используется в Starburst [MP94]. Выбираемая SIPS «соответствует» порядку соединений, который происходит из оптимизации исходного запроса без магической перезаписи. Для этой эвристики не было представлено никакого оценочного обоснования, нет и никакой гарантии, что выбирается хороший план. На самом деле, как мы покажем в разд. 6, эта эвристика может приводить к плохому выбору. Однако, поскольку исходный запрос также независимо оптимизируется, можно гарантировать, что перезапись на основе магических множеств не приведет к ухудшению производительности.
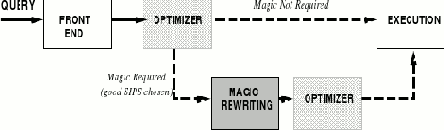
Рис. 3. Архитектура оптимизации
Аннотация
Перезапись с использованием магических множеств является хорошо известной оптимизационной эвристикой для сложных запросов принятия решений. Даже для простого запроса может иметься много вариантов этой перезаписи, сильно различающихся по эффективности выполнения. Мы предлагаем основанные на стоимости методы для выбора эффективного варианта из многих альтернатив.
Нашим первым вкладом является практическая схема моделирования перезаписи с использованием магических множеств как специального метода соединений, который можно добавить к любому оценочному оптимизатору. Мы выводим оценочные формулы, позволяющие оптимизатору выбрать наилучший вариант перезаписи и решить, полезен ли он. Порядок сложности процесса оптимизации сохраняется путем ограничения пространства поиска разумным образом. Мы реализовали этот метод в системе баз данных IBM DB2 C/S V2. Наши измерения производительности показывают, что оценочный метод оптимизации с использованием магических множеств работает хорошо, и что без его использования могли бы быть приняты некоторые ложные решения.
Вторым вкладом является формальная алгебраическая модель перезаписи с использованием магических множеств, основанная на расширении мультимножественной реляционной алгебры. Мы вводим мультимножественную операцию ?-полусоединения и получаем правила эквивалентности, включающие эту операцию. Мы демонстрируем, что перезапись с использованием магических множеств для не рекурсивных SQL-запросов можно моделировать как последовательную композицию этих правил эквивалентности.
Букварь по оптимизации соединений
Оптимизатор запросов определяет эффективный порядок, в котором следует производить соединения N отношений, и метод, используемый для каждого соединения. Поскольку операция соединения ассоциативна и коммутативна, имеется обширное пространство из O((2(N-1))!/(N-1)!) возможных порядков соединений [GHK92]. Поскольку это пространство недопустимо обширно для целей анализа даже для небольших значений N, в большинстве практических алгоритмов оптимизации соединений [SAC+79, IK84, KBZ86] анализируются ограниченные области этого пространства. У всех алгоритмов имеется одна общая черта: на каждом шаге в них рассматриваются различные двухместные соединения, и для каждого соединения анализируется стоимость применения различных методов соединения.
CM-преобразование SQL-блока с использованием
?-полусоединения: Алгебраическое выражение V, генерируемое путем преобразования SQL-запроса, состоящего из одиночного блока запроса, имеет вид:
При наличии фильтрующего отношения F для V, обозначаемого V ?<? F, к V ?<? F можно применить следующую последовательность преобразований. Во-первых, определим наиболее мощное подмножество ?, обозначаемое как ?n, которое можно протолкнуть через операцию группировки/агрегации. Если в исходном запросе не использовался раздел GROUPBY, то предикат ?n является таким же, как и ?. Затем
Наконец, можно многократно применить шаг CMT к выражению
как это описывается ниже. Сначала определим Si, i ? 1 следующим образом:

Кроме того, пусть ?i, i < n обозначает наиболее мощное подмножество ?i+1, в котором используются только атрибуты F и Si, а ?i, i < n обозначает оставшуюся часть ?i+1. Первое применение шага CMT преобразует
Посмотрим теперь на S’n-1: ?-полусоединение можно протолкнуть через определение S’n-1 точно в такой же манере, как выше. Таким образом, шаг CMT применяется для каждого Si, n ? i ? 2. Заметим, что имеются два вхождения S’n-1, т.е. это общее подвыражение двух выражений. Путем использования помеченных выражений мы можем избежать двойной оптимизации и вычисления выражений. Использование помеченных выражений является очень важным для избежания экспоненциального взрыва при спуске от Sn к S1.
CM-преобразование SQL-запросов с представлениями:
Мы начинаем с блока SQL-запроса и выполняем преобразование ?-полусоединение, как это описывалось раньше. В этом блоке могут использоваться представляемые отношения, и после преобразования использования отношения Ri в блоке может иметься полусоединение вида
Обсуждавшаяся ранее для случая одиночного соединения связь между шагом CMT и ограничительной магической перезаписью также распространяется на случай соединений и запросов над несколькими представлениями.
Таким образом, мы показали, что для SQL-запросов эффект ограничительной магической перезаписи достигается как специальный случай преобразований ?-полусоединений, в частности, путем использования шага CMT. При исследовании полного пространства эквивалентных выражений ограничительная магическая перезапись будет рассматриваться в качестве варианта, и в пространстве поиска будет выбрано наиболее дешевое выражение.
Фиксированные варианты SIPS
Диаграмма на рис. 6 показывает эффективность различных фиксированных вариантов SIPS для перезаписи на основе магических множеств. При существующем состоянии дел требуется, что пользователь базы данных выбрал один такой вариант для каждого запроса. Как показывает диаграмма, наилучшие варианты существенно отличаются для разных запросов, хотя единственным реальным различием между запросами являются предикаты на соответствующих таблицах. Сравнение диаграмм на рис. 5 и 6 показывает, что для каждого запроса выбор magopt близок к наилучшему варианту; алгоритм формирует нижнюю огибающую доступных вариантов. В этом состоит отдельный важный результат данной статьи; он мотивирует нашу работу и демонстрирует успех нашего подхода.

Рис. 7. Общее время компиляции
Измерение производительности
Цели нашего изучения производительности состояли в следующем: (1) Показать, что для магической перезаписи существуют различные варианты выбора SIPS, и что никакой конкретный вариант выбора SIPS не является оптимальным для всех запросов и сред выполнения. (2) Показать, что оценочная магическая оптимизация обеспечивает выбор, близкий к оптимальному, для различных запросов и сред выполнения. (3) Показать, что дополнительные накладные расходы, порождаемые оценочной магической оптимизацией, не влияют на порядок сложности процесса оптимизации.
К сожалению, нет «стандартного» тестового набора для оценивания методов, подобных перезаписи на основе магических множеств. Взамен нам пришлось изобретать для этой цели экспериментальную методологию. Выбираемые нами эксперименты должны были быть относительно простыми для понимания и разъяснения. Более того, мы должны были смочь исследовать различные измерения перезаписи на основе магических множеств за небольшое число экспериментов. В следующем разделе описывается наша попытка изобретения такой методологии.
Эффективность
Мы изучали эффективность нашего алгоритма, используя контролируемые эксперименты, подробно описываемые в следующем разделе. Основное заключение состоит в том, что результаты вполне отвечают нашим ожиданиям. Оценочная оптимизация предотвращает использование перезаписи на основе магических множеств, когда этого делать не следует, и позволяет выбрать один из лучших вариантов, когда перезапись на основе магических множеств целесообразно применять. Более того, эти положительные результаты получены без изменения порядка сложности оптимизации.
Экспериментальная методология
Тестовый набор TPC-D является общеотраслевым стандартным тестовым набором для сложных запросов [TPCD94]. В тестовом наборе имеются два запроса, к которым может быть применена перезапись на основе магических множеств (Query 2 и Query 17). Нас интересовал Query 2, потому что для него имеется большое число вариантов магической перезаписи (он включает соединение многих отношений), в то время как для другого кандидата (Query 17) имеется только один вариант.
В первом эксперименте стартовой точкой является Query 2 из TPC-D. Во внешнем блоке запроса предикаты выборки постепенно изменялись путем их удаления, модификации с целью уменьшения селективности или замены на менее селективные предикаты. Эффект состоял в том, что мощность результата запроса постепенно увеличивалась. Однако реальные таблицы в запросе не изменялись, так что всегда был возможен выбор одних и тех же вариантов SIPS. По мере изменения предикатов разные варианты выбора SIPS становятся оптимальными, и иногда бывает лучше вообще не производить магическую перезапись. Мощность результата запроса грубо связана с возможным эффектом фильтрации вследствие магических множеств; следовательно, мы ожидаем большей пользы от перезаписи на основе магических множеств при меньшей мощности результата. Оптимизатор, усовершенствованный оценочной магической оптимизацией, должен всегда выбирать правильные SIPS для всех запросов.
Мы полностью повторили эксперимент после модификации исходного запроса, использованного в качестве стартовой точки (путем изменения содержимого внутреннего блока запроса). Тем самым, мы смогли исследовать воздействия на разнообразные запросы в контролируемой и понятной манере. Мы также повторили эксперимент после ликвидации некоторых индексов, использованных в исходных планах; это представляет изменение в среде выполнения. Следовательно, изменяется стоимость различных частей запроса. Оценочная магическая оптимизация должна быть в состоянии это распознавать и принимать правильное решение в новой среде.
Эксперименты производились на рабочей станции IBM RS/6000, подключенной к двум дискам. База данных TPCD объемом в 100 Мб (т.е. с коэффициентом масштабирования 0.1 в соответствии со стандартом TPCD) была сгенерирована со всеми уместными индексами. На оси X графиков результатов отмечены варианты запросов, упорядоченные по возрастанию размера результата. В качестве основной метрики производительности использовалось время выполнения запроса. Заметим, что в графиках времени выполнения используется логарифмическая шкала, так что кажущиеся небольшими различия в действительности достаточно значительны. Мы также измеряли время компиляции запроса, чтобы показать накладные расходы на дополнительную работу оптимизатора. Все временные показатели единообразно масштабированы поправочным множителем.
Как исчезает сложность?
Хотя имеется экспоненциальное число возможных вариантов перезаписи, мы ухитряемся произвести поиск наилучшего плана за два вызова оптимизатора: один – для нахождения наилучшей SIPS, а другой – для оптимизации запроса, перезаписанного на основе этой SIPS. Важно понимать, как исчезает исходная сложность; здесь нет никакой магии! В разд. 3.4 накладываются некоторые ограничения на исследуемое пространство поиска. Например, для примера из разд. 2 не будет оцениваться стоимость следующего варианта магической перезаписи: Dept используется как таблица PartialResult, и отфильтрованная версия представления LimitedDepAvgSal сначала соединяется с Emp, а потом с Dept. Другой используемый метод состоял в получении «хорошей оценки» стоимости параметризуемых планов вместо их явного вычисления. Хотя наши оценки являются, несомненно, приблизительными, это существенно лучше полного отсутствия оценок (а именно таково текущее состояние дел с алгоритмами, подобными магическим множествам). Коротко говоря, мы утверждаем, что, весьма вероятно, использование этих методов улучшит результаты сегодняшних оптимизаторов запросов. Реализация в системе баз данных DB2 C/S V2 эмпирически подтверждает верность этого утверждения.
Магические множества и оптимизация соединений
В этом разделе мы опишем, каким образом выбор вариантов перезаписи на основе магических множеств можно рассматривать как часть фазы оптимизации соединений оптимизатора запросов.
Мотивация
SQL-запрос на рис. 1 находит всех работающих в больших отделах молодых служащих, зарплата каждого из которых выше средней зарплаты отдела, в котором работает данный служащий. Запрос затрагивает реляционное представление DepAvgSal, которое порождает среднюю зарплату в каждом отделе, и включает соединение отношений Emp, Dept и DepAvgSal. В перезаписи на основе магических множеств используется тот факт, что среднюю отдельскую зарплату не требуется вычислять для каждого отдела; ее нужно вычислять только для больших отделов, в которых имеются молодые служащие. Если таких отделов немного, то, вероятно, желательно применить перезапись на основе магических множеств. Переписанный запрос показан на рис. 2. Представление PartialResult представляет представляет частичное вычисление в основном блоке запроса на стадии, когда таблицы Emp и Dept уже соединены между собой, но к ним еще не присоединено представление DepAvgSal. На основе этой таблицы PartialResult создается не содержащее дубликатов представление Filter, порождающее множество всех отделов, для которых требуется вычислять среднюю зарплату. Далее это фильтрующее множество используется для ограничения вычислений в исходном представлении. Представление модифицируется путем включения эквисоединения с фильтрующим множеством (тем самым, ограничивая вычисления в представлении отделами, представляющими интерес). Наконец, в основном блоке запроса на рис. 2 модифицированное представление соединяется с таблицей PartialResult для формирования окончательного результата.
Нотация
Мы используем символы R (с нижним регистром или без него) для обозначения отношений, ? (с нижним регистром или без него) для обозначения предикатов, E (с нижним регистром или без него) для обозначения реляционных выражений, attrs(E) для обозначения атрибутов результата E и a для обозначения кортежа атрибутов. В соответствии с семантикой SQL мы трактуем отношения как мультимножества кортежей и используем мультимножественный вариант реляционной алгебры [DGK82]. Мы предполагаем знакомство читателей с этой алгеброй и описываем только операцию группирования/агрегации и мультимножественную операцию ?-полусоединения. Мы используем операцию группирования/агрегации g? f , где g обозначает атрибуты группирования, а f – агрегатные операции, которые выполняются над группами, определяемыми атрибутами группирования. (Эта нотация заимствована из [EN94, Klu82]; такая операция требуется для работы с группировкой и агрегированием в стиле SQL.)
Общие результаты
Графики на рис. 5 показывают общие результаты измерения производительности. Оптимизация путем магической перезаписи на основе Filterjoin (т.е. magopt) может сильно повысить скорость выполнения запросов по сравнению с nomag. Так происходит при небольших размерах результата, поскольку в этом случае и фильтрующее множество является небольшим и достаточно селективным. Это позволяет ограничить вычисление сложного представления и тем самым сократить время выполнения. Однако, если размер фильтрующего множества возрастает, его преимущества медленно уменьшаются, а стоимость растет, так что в последней точке графика (размер 11986) алгоритм перестает выполнять перезапись на основе магических множеств. Это объясняет, почему в последней точке значения времени одинаковы для nomag и magopt. Алгоритм sbmag хорошо работает для более крупных запросов, на с двумя наиболее мелкими запросами справляется плохо. Чтобы понять причины такого поведения sbmag, обратим внимание на тот факт, что оптимизатор трактует сложное представление как временное отношение без индексов. Если другие соединения в запросе очень селективны, и другие отношения проиндексированы, то в наиболее дешевом плане представление часто ставится в начало порядка соединений. Основываясь на этом плане, sbmag принимает решение не использовать магические множества. Однако это именно те запросы, для которых можно ожидать наибольшей пользы от магии!
Интересный предмет для обсуждения представляет четвертый запрос (размер 236) на рис. 5. Мы видим, что производительность magopt слегка хуже, чем у nomag. Очевидно, что оптимизатор, выбирая для magopt магическую перезапись, ожидал, что результат будет лучше, чем у nomag. Это показывает, что оценки стоимости, принимаемые оптимизатором, отличаются от реальной стоимости из-за неточных статистики и/или предположений. Алгоритмы, подобные оценочной магической оптимизации, построенные поверх этих ошибок, могут время от времени могут приводить к неоптимальной производительности.

Рис. 6. Варианты перезаписи на основе магических множеств
Обсуждение
В нескольких коммерческих системах баз данных используются идентификаторы кортежей (tid) как неявные атрибуты, позволяющие различить множественные вхождения кортежа. В этих системах выполняются преобразования SQL-запросов, которые могут влиять на мультимножественную семантику (например, замена вложенных подзапросов соединениями), и уникальные tid’ы используются, в случае потребности, для получения корректной семантики. Это делается следующим образом. Для отношений, перечисленных в разделе FROM, т.е. для тех отношений, которые вносят вклад в мультимножественную семантику, tid’ы выбираются вместе со всеми другими атрибутами, встречающимися в разделе SELECT, и в результирующем отношении производится удаление дубликатов. На заключительной фазе выполняется проецирование, устраняющее атрибуты-tid’ы, и получается желаемое мультимножественное отношение.
Этот подход обладает тем преимуществом использования соединений, а не ?-полусоединений, что позволяется использовать большее число порядков соединения. Однако у него имеется несколько недостатков. Во-первых, его невозможно использовать в связи с группировкой/агрегированием. Во-вторых, оптимизатор должен отслеживать tid’ы при выполнении операций и производить удаление дубликатов. Наш подход использования операции ?-полусоединения является более чистым, поскольку он может единообразно справляться как с SQL-запросами с мультимножественной семантикой, так и с запросами с множественной семантикой. Кроме того, наш запрос позволяет избежать расходов на явное удаление дубликатов и на поддержку tid’ов и работу с ними.
Оценивание FilterCostRk
Чтобы моделировать перезапись на основе магических множеств как Filterjoin и получать оценку его стоимости, нам не требуется явно планировать модифицированное внутреннее представление. Нам нужно всего лишь оценить мощность модифицированного представления и стоимость наилучшего плана его генерирования. На этой стадии не нужен реальный план, потому что в архитектуре оптимизации, представленной в разд. 2.2, требуется второй проход оптимизации после выполнения магической перезаписи. Размер фильтрующего воздействия фильтрующего множества (т.е. его селективность) зависит от его мощности. Поскольку точно оценить мощность проекции трудно [LNSS93], в существующих оптимизаторах принимаются некоторые предположения для оценки мощности проекции [Yao77].
Нам требуется параметризованный план для ограничения Rk, параметром которого является фильтрующее множество. Далее, нам хотелось бы иметь возможность генерировать параметризуемый план только один раз. Каждый конкретный план получается путем параметризации плана конкретным фильтрующим множеством. По экземпляру плана можно получить его стоимость и мощность результата. Поскольку параметризуемая оптимизация запросов является темой проводимого в данное время исследования [INSS92], результаты носят слишком предварительный характер, чтобы их можно было применить к нашей проблеме. Нам нужен конкретный метод для работы с параметризацией в нашем контексте. Тривиальное решение состоит в том, чтобы выполнять вложенный вызов оптимизатора при создании каждого экземпляра плана. Однако время создания каждого экземпляра должно быть небольшой константой, а поскольку Rk может сложным выражением, включающим несколько соединений, этого добиться невозможно.
Заметим, что мощность отфильтрованного внутреннего отношения Rk’ является функцией только от селективности фильтрующего множества (которая известна) и не зависит от физического размера или реализации фильтрующего множества. После того как мощность Rk’ подсчитана для нескольких значений селективности F, можно соединить полученные точки линией, определяя тем самым функцию мощности Rk’ для всех фильтрующих множеств.
В действительности, в своей реализации мы решили вычислять всего две точки и производить прямую линейную интерполяцию. Выбранные точки соответствуют селективности 0 (когда мощность результата, очевидно, равняется нулю) и 1 (когда мощность результата совпадает с мощностью не модифицированного представления Rk).
Оценивание стоимости Rk’ является более сложным, потому что функции стоимости соединений могут быть нелинейными, особенно в границах размеров, когда отношение перестает помещаться в основной памяти, доступной для некоторой операции. Поэтому простая линейная интерполяция может быть неточной. Один из подходов состоит в том, чтобы определить несколько классов эквивалентности на основе размера магического множества (например, «меньше размера буфера» и «больше размера буфера») и внутри каждого класса использовать прямую линейную интерполяцию. Следует заметить, что на практике фильтрующие множества обычно бывают небольшими, поскольку содержат проекцию (без дубликатов) только на столбец соединения. Поэтому простая линейная интерполяция может выполняться удовлетворительным образом; на самом деле, в своем прототипной реализации мы использовали именно этот метод.
Оценка стоимости и мощности
Теперь мы выведем формулу для оценки стоимости применения метода Filterjoin. Заметим, что эта оценочная формула должна вычисляться за константное время. Предположим, что в оцениваемом Filterjoin имеются (R1 ?? R2 ?? … ?? R(k-1)) как внешнее отношение и Rk как внутреннее отношение. Стоимость вычисления соединения можно разбить на компоненты, показанные в таб. 1 и разъясняемые ниже. Общая стоимость Filterjoin является суммой этих компонентов.
JoinCostP + ProductionCostP + ProjCostF +
FilterCostRk + FinalJoinCost
JoinCostP: Это стоимость внешнего отношения, которая уже вычислялась как часть алгоритма оптимизации.
ProductionCostP: P требуется материализовать, поскольку это отношение используется как для генерации фильтрующего множества, так и в соединении верхнего уровня. Стоимость материализации PartialResult – это простая функция от мощности P. Поскольку эта мощность уже известна (т.е. уже оценена оптимизатором), можно вычислить стоимость материализации. Вместо того чтобы создавать временное отношение P, можно было бы вычислять повторно. Стоимость повторного вычисления P является такой же, как и JoinCostP. В качестве ProductionCostP выбирается минимум из стоимости материализации и стоимости повторного вычисления.
ProjCostF: Стоимость выполнения проецирования P (с устранением дубликатов) для генерации фильтрующего множества F зависит от мощности P. Эта стоимость также зависит от физических характеристик плана для P (например, отсортировано P или нет) и от того, можно ли совместить проецирования с генерацией P. У оптимизатора имеется вся необходимая информация для оценивания ProjCostF.
FilterCostRk: Это стоимость генерации отфильтрованной версии Rk с использованием фильтрующего множества F (пусть отфильтрованное отношение называется Rk’). Обсуждение метода вычисления стоимости и мощности Rk’ приводится после этих определений.
FinalJoinCost: Это считается просто. Мощность внешнего отношения известна. Мощность отфильтрованного внутреннего отношения только что подсчитана. Для определения наиболее дешевого способа выполнения завершающего соединения можно применить оценочные формулы других доступных методов соединения.
Заметим, что все (кроме одного) компоненты стоимости можно вычислить за константное время с использованием общеизвестных оценочных формул, уже используемых в существующих оценочных оптимизаторах. В следующем разделе показывается, как можно оценить за константное время стоимость и мощность отфильтрованного отношения Rk (FilterCostRk).
Оценочная модель для ?-полусоединения
Операцию ?-полусоединения R1 ?<? R2 можно эффективно реализовать с использованием небольших изменений таких методов соединения, как соединение с хэшированием и индексное соединение. В одной из реализаций левый операнд R1 ?-полусоединения трактуется как «внешнее» отношение метода соединения. Для каждого кортежа внешнего отношения R1, вместо того чтобы соединять его с каждым подходящим кортежем внутреннего отношения R2, этот кортеж поступает в результат операции, как только обнаружено соответствие. Аналогичным образом для реализации ?-полусоединений можно приспособить метод соединения сортировкой со слиянием, если предикатом соединения является равенство.
В качестве альтернативы в методе соединения можно трактовать как «внешнее» отношение правый операнд R1 ?-полусоединения. Для каждого кортежа внешнего отношения R2 возвращаются все подходящие кортежи внутреннего отношения R1. Если кортеж из R1 уже находится в результате вследствие соответствия другому кортежу R2, то он не добавляется к результату; для эффективной реализации в общем случае требуется наличие индекса на результате ?-полусоединения. Если предикат ?-полусоединения включает равенство с суперключом R2, то это гарантирует, что любой кортеж R1 соответствует не более чем одному кортежу R2; в этом случае не требуется какой-либо индекс на результате ?-полусоединения.
Оценочные формулы для различных методов соединения легко модифицируются для порождения оценочных формул для различных способов реализации операции ?-полусоединения. Мы опускаем детали. На оценочной фазе трансформационного оптимизатора, такого как Volcano, используются оценочные формулы для операций алгебры, чтобы вычислить оценки стоимости для различных способов вычисления запроса.
Поскольку ?-полусоединение является порождаемой операцией (ее можно выразить с использованием ?-соединения, проекции и удаления дубликатов), ее можно также реализовать с использованием алгоритмов для этих операций. Однако такая реализация является неэффективной.
Оценочная оптимизация для магии: алгебра и реализация
Правин Сешарди (, Univ. of Wisconsin, Madison)
Джозеф Хеллерстейн (, Univ. of California, Berkeley)
Хамид Пирамеш (, IBM Almaden Research Ctr.)
Клифф Леюнг (, IBM Santa Teresa Lab.)
Раджу Рамакришнан (, Univ. of Wisconsin, Madison)
Дивеш Сривастава (, AT&T Research)
Питер Стюки (, Univ. of Melbourne)
С. Сударшан (, IIT, Bombay)
SIGMOD Conference 1996: 435-446
Перевод: Сергей Кузнецов
Правин Сешарди (, Univ. of Wisconsin, Madison)
Джозеф Хеллерстейн (, Univ. of California, Berkeley)
Хамид Пирамеш (, IBM Almaden Research Ctr.)
Клифф Леюнг (, IBM Santa Teresa Lab.)
Раджу Рамакришнан (, Univ. of Wisconsin, Madison)
Дивеш Сривастава (, AT&T Research)
Питер Стюки (, Univ. of Melbourne)
С. Сударшан (, IIT, Bombay)
SIGMOD Conference 1996: 435-446
Перевод: Сергей Кузнецов
Правин Сешарди (, Univ. of Wisconsin, Madison)
Джозеф Хеллерстейн (, Univ. of California, Berkeley)
Хамид Пирамеш (, IBM Almaden Research Ctr.)
Клифф Леюнг (, IBM Santa Teresa Lab.)
Раджу Рамакришнан (, Univ. of Wisconsin, Madison)
Дивеш Сривастава (, AT&T Research)
Питер Стюки (, Univ. of Melbourne)
С. Сударшан (, IIT, Bombay)
SIGMOD Conference 1996: 435-446
Перевод: Сергей Кузнецов
Правин Сешарди (, Univ. of Wisconsin, Madison)
Джозеф Хеллерстейн (, Univ. of California, Berkeley)
Хамид Пирамеш (, IBM Almaden Research Ctr.)
Клифф Леюнг (, IBM Santa Teresa Lab.)
Раджу Рамакришнан (, Univ. of Wisconsin, Madison)
Дивеш Сривастава (, AT&T Research)
Питер Стюки (, Univ. of Melbourne)
С. Сударшан (, IIT, Bombay)
SIGMOD Conference 1996: 435-446
Перевод: Сергей Кузнецов
Правин Сешарди (, Univ. of Wisconsin, Madison)
Джозеф Хеллерстейн (, Univ. of California, Berkeley)
Хамид Пирамеш (, IBM Almaden Research Ctr.)
Клифф Леюнг (, IBM Santa Teresa Lab.)
Раджу Рамакришнан (, Univ. of Wisconsin, Madison)
Дивеш Сривастава (, AT&T Research)
Питер Стюки (, Univ. of Melbourne)
С. Сударшан (, IIT, Bombay)
SIGMOD Conference 1996: 435-446
Перевод: Сергей Кузнецов
Оценочное решение
В данной статье представляется оценочное решение проблемы выбора надлежащей SIPS. Мы реализовали свое решения в системе баз данных DB2 C/S V2 (основанной на системе Starburst [HCL+90]), в которой поддерживается перезапись на основе магических множеств как преобразование «запрос-в-запрос». Архитектура системы показана на рис. 3. Пользовательский запрос поступает прямо на вход оценочного оптимизатора, который решает, выполнять или нет перезапись на основе магических множеств. В то время когда оптимизатор анализирует пространство возможных порядков и методов соединений, он также исследует и пространство возможных вариантов для перезаписи на основе магических множеств. Если принимается решение о том, что никакая перезапись не требуется, оптимизатор генерирует план выполнения обычным образом и посылает его процессору выполнения. С другой стороны, если оптимизатор решает, что магическая перезапись требуется, то он также выбирает одну конкретную SIPS для перезаписи, которая руководит применением преобразования на основе магических множеств. После того, как запрос перезаписывается, он снова оптимизируется для генерации плана выполнения. В обсуждавшемся выше решении Starburst [MP94] впервые предлагалась двухпроходная архитектура, и мы используем ту же идею, поскольку хотели бы избежать серьезных изменений в существующих компонентах системы. Альтернативный подход, который мы обсуждаем в разд. 7, состоит в реализации магической перезаписи с помощью алгебраических преобразований (вместо перезаписи «SQL-в-SQL»).
1 При наличии многих вариантов перезаписи на основе магических множеств наиболее практичным подходом в контексте РСУБД является перезапись на основе дополнительных магических множеств, используемая в этой статье.
2 В литературе фильтрующее множество и PartialResult называются «магическим» множеством и «дополнительным» магическим множеством соответственно.
Ограничение пространства поиска
Пространство опций для одного конкретного Filterjoin является обширным по трем причинам:
Имеется много возможных вариантов выбора для PartialResult. Вообще говоря, если составное внешнее отношение образуется путем соединения (k-1)-го отношения, то любое подмножество из 2(k-1)-1 непустых подмножеств множества этих отношений могло бы использоваться в качестве основы PartialResult. При наличии конкретного PartialResult имеется много возможных вариантов выбора для фильтрующего множества. Вообще говоря, если имеется m атрибутов соединения, то любое подмножество из 2m-1 непустых подмножеств множества этих атрибутов могло бы использоваться в качестве основы фильтрующего множества. Кроме того, могло бы иметься несколько возможных реализаций фильтрующего множества (например, как отношение или как фильтр Блюма). При наличии конкретного фильтрующего множества имеется обширное пространство возможных планов для внутреннего реляционного представления, модифицированного путем добавления фильтрующего множества.
Пункты (1) и (2) приводят к полному диапазону SIPS, обсуждавшемуся в [BR91]. Перед лицом громадных пространств поиска мы заимствуем два хорошо известных и широко используемых метода оптимизации: (a) На пространстве поиска для Filterjoin мы применяем эвристические ограничения. Будем надеяться, что большая часть пространства поиска, отбрасываемая эвристиками, не представляет интереса. (b) Мы принимаем предположения, позволяющие нам использовать приемлемо точные «интуитивные оценки» («guesstimates») стоимости для частей пространства поиска вместо того, чтобы действительно анализировать эти части и вычислять более точные оценки.
Определение 3.1 (R Filter-Join S)
R называется внешним отношением, а S – внутренним отношением метода Filter-Join. Создается надмножество (без дубликатов) значений атрибута соединения R и используется как фильтр для ограничения кортежей S, к которым производится доступ. Ограниченное отношение из кортежей S затем соединяется с отношением R (с использованием любого другого доступного алгоритма соединения).
Этот метод соединения похож на хорошо известную операцию полусоединения [BGW+81], и эта схожесть используется в разд. 7 при моделировании магических множеств с использованием операции ?-полусоединения. Важным отличием является то, что полусоединения обычно применяются к хранимым отношениям, в то время как перезапись на основе магических множеств работает с представлениями.
Предположим, что оптимизатор запросов, дополненный возможностью рассмотрения Filterjoin как метода соединения, вызывается для обработки запроса с соединением N отношений. На некоторой промежуточной стадии оптимизатор оценивает стоимость некоторого соединения. Внешнее соединение является составным отношением вида (R1 ?? R2 ?? … ?? R(k-1)), и внутренним является одиночное отношение Rk, для которого можно применить перезапись на основе магических множеств (т.е. Rk является представлением). Наименьшее фильтрующее множество будет происходить из проекции (без дубликатов) всего составного внешнего отношения. Менее ограничительные фильтрующие множества могли бы создаваться путем использования в качестве PartialResult соединения любого подмножества таблиц составного внешнего отношения. После того как сделан конкретный выбор PartialResult, само фильтрующее множество может быть представлено точно или с некоторыми потерями (т.е. взамен может использоваться некоторое надмножество фильтрующего множества) путем опускания некоторых атрибутов соединения.
Имеется много различных вариантов выбора для PartialResult и для фильтрующего множества. Как мы показали в Примере 2, фильтрующее множество используется для ограничения внутреннего отношения путем добавления этого множества в раздел FROM внутреннего блока запроса. Даже после выбора некоторого PartialResult и некоторого фильтрующего множества модифицированная версия внутреннего реляционного представления (LimitedDepAvgSal на рис. 2) нуждается в планировании. Ясно, что если эти варианты выбора исследуются для каждого возможного соединения, включающего Rk, то мы проанализируем все возможные комбинации SIPS. Однако мы не склонны к тому, чтобы подвергать риску сложность оптимизатора ради оптимизирующей перезаписи на основе магических множеств. Из этого следует, что если мы предлагаем анализировать возможные варианты выбора для каждого Filterjoin, то это должно делаться за константное время. Поэтому наша следующая задача состоит в сокращении пространства поиска до некоторых приемлемых размеров.
Определение 7.1 (Мультимножественное
?-полусоединение) Мультимножественный вариант операции ?-полусоединения ?<? определяется следующим образом. Для двух заданных отношений R1 и R2
где ?(t2) обозначает предикат ?, в котором имена атрибутов из R2 заменены их значениями из кортежа t2.
Определение ?-полусоединения сохраняет семантику семантику мультимножеств, т.е. кратность каждого кортежа, присутствующего в результате, совпадает с кратностью этого кортежа в R1. Например, если отношение R1(A,B) является мультимножеством кортежей {(1,2), (1,2), (1,4), и R2(C,D) состоит из {(3,5), (3,6), (3,7)}, то R1 ?<C?D R2 = {(1,2), (1,2)}.
В мультимножественной реляционной алгебре ?-полусоединение является выводимой операцией, выражаемой через операции ?-соединения, проекции (?) и удаления дубликатов (?) следующим образом:
где ?? Nat обозначает естественное соединение. Интуитивно понятно, что выражение
содержит все кортежи результата ?-полусоединения, но, возможно, с неверной кратностью. Следующая за естественным соединением операция удаления дубликатов используется для восстановления желаемой кратности.
В некоторых из описываемых нами правил эквивалентности ?-полусоединений используются присутствующие в отношениях функциональные зависимости; мы обозначаем функциональные зависимости, присутствующие в отношении R, как FD(R). Кроме того, в правилах эквивалентности также используются функциональные зависимости, следующие из предикатов (таких как предикаты ?-соединения и ?-полусоединения). Например, из предиката x = y * y следует функциональная зависимость {y} > x, а из предиката x = y + z следуют функциональные зависимости {y,z} > x, {x,y} > z и {x,z} > y. Мы используем нотацию FD(?) для обозначения множества всех функциональных зависимостей, следующих из предиката ?.
Осуществимость
Мы прототипировали предложенную оценочную оптимизацию на внутренней версии IBM системы баз данных DB2 C/S V2. Хотя в оптимизаторе запросов поддерживаются различные стратегии поиска, мы сосредоточились на стратегии, в которой используется общеизвестный алгоритм оптимизации методом динамического программирования «слева-вглубь». Выбрав полностью зрелую систему, мы были вынуждены столкнуться со всеми практическими ограничениями, существующими в реальной СУБД. Один из нас работал на DB2 C/S V2 над созданием прототипа перезаписи но основе магических множеств. Несмотря на исходное отсутствие знакомства с кодом оптимизатора, модификации и измерения производительности были завершены за три месяца. Хотя требовались изменения во многих частях оптимизатора, реальное число строк добавленного кода на C++ составило меньше 1000. Мы полагаем, что это подтверждает возможность добавления метода Filterjoin к существующим оптимизаторам.
Перезапись на основе магических множеств как метод соединения
Мы определяем Filter-Join отношений R и S следующим образом:
Практический опыт
Мы обнаружили, что перезапись на основе магических множеств действует на оптимизатор запросов как «нагрузочные испытания» («stresstest»). Это связано с тем, что в данном методе используются общие подвыражения, проецирование с удалением дубликатов, временные отношения и другие элементы, которые обычно применяются только в сложных запросах поддержки принятия решений. Поэтому, наряду с тем, что оценка стоимости для перезаписи на основе магических множеств определенно осмысленна на логическом уровне, важно, чтобы оптимизатор правильно моделировал конструкции, используемые при перезаписи.
3 Другим способом введения избыточности является использования фильтра Блюма (Bloom filter) [Blo70] для реализации фильтрующего множества.
Правила преобразований для ?-полусоединения
Оптимизация SQL-запросов на основе использования ?-полусоединений включает спецификацию правил эквивалентности выражений с полусоединениями и другими операциями расширенной мультимножественной реляционной алгебры. При наличии набора правил эквивалентности может быть использован трансформационный оптимизатор, такой как Volcano [GM93], для перечисления и компактного представления логического пространства поиска. Для вычисления оценок стоимости и выбора оптимального способа вычисления запроса используются оценочные формулы.
Ниже мы обсудим некоторые наиболее интересные преобразования выражений с операциями ?-полусоединений и ?-соединений; остальные правила представлены в [SSS95]. В алгебраических преобразованиях может потребоваться шаг переименования, например, при изменении структуры выражений. Как и в других подобных работах, для простоты изложения мы игнорируем шаг переименования в своих правилах эквивалентности; детали переименования можно легко разработать самостоятельно.
Предположение 1:
Стоимость и мощность результата Filter-join могут быть оценены за константное время.
Если предположение 1 справедливо, то порядок сложности оптимизации соединений не изменяется, хотя Filterjoin учитывается в качестве варианта. Для каждого конкретного соединения в методе Filterjoin рассматривается только одно отношение PartialResult и небольшое константное число фильтрующих множеств, и стоимость Filterjoin определяется за константное время. Весь запрос оптимизируется, и рассматривается наиболее дешевый полный план. Если он не содержит Filterjoin, то перезапись на основе магических множеств применять не следует; иначе производится перезапись с использованием SIPS, специфицируемую составным внешним отношением Filterjoin.
| JoinCostp | Стоимость выполнения соединений, требуемых для генерации PartialResult P |
| ProductionCostp | Стоимость материализации PartialResult P |
| ProjCostF | Стоимость проецирования P для генерации фильтрующего множества F |
| FilterCostRk | Стоимость генерации Rk и его ограничения с использованием фильтрующего множества |
| FinalJoinCost | Стоимость выполнения завершающего соединения внешнего отношения и Rk’ |
Таб. 1. Компоненты стоимости Filterjoin
Применение правил эквивалентности ?-полусоединения
Перезапись с использованием правил эквивалентности ?-полусоединения особенно полезна для сложных запросов, в которых используются представления, не развертываемые в соединения. В число примеров входят:
Запросы, в которых используются представления, определенные с применением агрегации. Пример такого запроса был представлен в разд. 2. Запросы над представлениями, в определениях которых используется SELECT DISTINCT. Такие представления развертываются в некоторых, но не во всех случаях. Запросы с внешними соединениями. Представления, используемые в качестве аргументов внешних соединений, развернуть невозможно.
Особым преимуществом оптимизации на основе правил является простота спецификации преобразований для разнообразных операций. В действительности, набор правил преобразования, представленный в [SSS95], обеспечивает возможность протолкнуть ?-полусоединения в представления во всех упомянутых примерах.
Если бы добавить к исчерпывающему оптимизатору полное множество правил эквивалентности ?-полусоединения, то пространство поиска могло бы очень сильно расшириться. Представленные выше классы запросов представляют наиболее важные классы применения правил эквивалентности ?-полусоединения, что приводит к следующей весьма полезной эвристике:
Операцию ?-полусоединения следует вводить только имея дело и операциями агрегации, устранения дубликатов и внешнего соединения.
Правило эквивалентности для агрегации было представлено выше, а другие правила описываются в [SSS95].
4 В множественном варианте реляцио нной алгебры ?-полусоединение можно выразить более просто, как
5 При трансляции SQL в реляционную алгебру, представленной в [CG85], ?-полусоединения используются только при обработке разделов HAVING.
Пространственная сложность оптимизации
Должно быть ясно, почему пространственная сложность не является предметом этой работы. При оптимизации основного блока запроса теперь нужно попробовать применить дополнительный метод для каждого анализируемого соединения. Однако для этого не требуется сохранять какие-либо дополнительные планы. Следовательно, рассмотрение дополнительного метода соединения не изменяет порядок пространственной сложности оптимизатора. Что касается «параметризуемого» планирования сложных представлений, то при нашем подходе оптимизируется отфильтрованная версия сложного запроса для небольшого константного числа классов эквивалентности. Следовательно, и это не приводит к изменению порядка пространственной сложности.
Проталкивание
?-полусоединения через соединение: Ниже мы представляем правило преобразования, описывающее, как протолкнуть ?-полусоединение через соединения.
где
Это преобразование позволяет использовать и E1, и E3 для ограничения кортежей, вычисляемых для E1’. Хотя в преобразовании используется декартово произведение, оно является полезным, если в некоторой части ?2 используются только атрибуты из E1 и E3 – эта часть ?2 может быть использована на последующем шаге для преобразования декартова произведения в ?-соединение. Интуитивные соображения по поводу корректности этого правила преобразования состоят в том, что требуются только те кортежи t2
Проталкивание
?-полусоединения через агрегирование: Следующее правило преобразования описывает, как протолкнуть ?-полусоединение через группировку и агрегирование.
где ? включает только атрибуты из g и atrrs(E2).
Здесь интуитивные соображения состоят в том, что если предикат полусоединения ? включает только атрибуты из g и atrrs(E2), то для каждой группы кортежей из E1 либо все кортежи будут выбраны при выполнении операции (E1 ?<? E2), либо не будет выбран ни один кортеж. Кортеж в результате операции ?, генерируемый для каждой группы, будет выбираться или не выбираться соответственно.
Если ? включает результаты агрегации, то операцию ?-полусоединения, вообще говоря, нельзя протолкнуть через агрегацию. В некоторых случаях, включающих min и max, операцию ?-полусоединения можно протолкнуть через g? f; см. [SSS95].
в предыдущих разделах, требуется для
Реализация алгоритма, представленного в предыдущих разделах, требуется для ответа на следующие вопросы: (1) Насколько возможно внедрить такой алгоритм в реальную систему баз данных? (2) Действительно ли алгоритм находит хорошие планы (т.е. работает ли он так, как ожидалось)?
References
[BGW+81] P. A. Bernstein, N. Goodman, E. Wong, C. L. Reeve and J. B. Rothnie. Query processing in a system for distributed databases (SDD1) ACM Transactions on Database Systems, 6(4):602--625, 1981.
[BMSU86] F. Bancilhon, D. Maier, Y. Sagiv and J. D. Ullman. Magic sets and other strange ways to execute logic programs. In Proceedings of the ACM Symposium on Principles of Database Systems, 1--15, 1986.
[BR91] C. Beeri and R. Ramakrishnan. On the power of Magic. Journal of Logic Programming, 10(3&4):255--300, 1991.
[Blo70] B. H. Bloom. Space/time tradeoffs in hash coding with allowable errors. Communications of the ACM, 13(7):422--426, 1970.
[CG85] S. Ceri and G. Gottlob. Translating SQL into relational algebra: Optimization, semantics,and equivalence of SQL queries. IEEE Transactions on Software Engineering, 11(4):324--345, 1985.
[DGK82] U. Dayal, N. Goodman, and R. H. Katz. An extended relational algebra with control over duplicate elimination. In Proceedings of the ACM Symposium on Principles of Database Systems, 1982.
[EN94] R. Elmasri and S. B. Navathe. Fundamentals of database systems. Benjamin/Cummings Publishers, 2nd edition, 1994.
[GHK92] S. Ganguly, W. Hasan and R. Krishnamurthy. Query optimization for parallel execution. In Proceedings of ACM SIGMOD International Conference on Management of Data, 1992.
[GM93] G. Graefe and W. J. McKenna. The Volcano optimizer generator: Extensibility and efficient search. In Proceedings of the IEEE International Conference on Data Engineering, 1993.
[HCL+90] L. Haas, W. Chang, G. M. Lohman, J. McPherson, P. F. Wilms, G. Lapis, B. Lindsay, H. Pirahesh, M. Carey, and E. Shekita. Starburst midflight: As the dust clears. IEEE Transactionson Knowledgeand Data Engineering, March 1990.
[Hel95] J. M. Hellerstein. Optimization and execution techniques for queries with expensive methods Ph.D. Thesis, University of Wisconsin, August 1995.
[IK84] T. Ibaraki and T. Kameda. Optimal nesting for computing Nrelational joins.
In ACM Transactions on Database Systems, 9(3):482--502, 1984.
[INSS92] Y. Ioannidis, R. Ng, K. Shim and T. K. Sellis. Parametric query optimization. In Proceedings of the International Conference on Very Large Databases (VLDB), 103--114, 1992.
[KBZ86] R. Krishnamurthy, H. Boral, and C. Zaniolo. Optimization of nonrecursive queries. In Proceedings of the International Conference on Very Large Databases (VLDB), 128--137, 1986.
[Klu82] A. Klug. Equivalence of relational algebra and relational calculus query languages having aggregate functions. Journal of the ACM, 29(3):699--717, 1982.
[LMH+85] G. M. Lohman, C. Mohan, L. M. Haas, D. Daniels, B. G. Lindsay, P. G. Selinger and P. F. Wilms. Query processing in R*. In Query Processing in Database Systems, (W. Kim, D. S. Reiner, and D. S. Batory, eds.), SpringerVerlag, 30--47, 1985.
[LNSS93] R. J. Lipton, J. F. Naughton, D. A. Schneider and S. Seshadri. Efficient sampling strategies for relational database operations. Theoretical Computer Science, 116:195--226, 1993.
[MFPR90] I. S. Mumick, S. Finkelstein, H. Pirahesh, and R. Ramakrishnan. Magic is relevant. In Proceedings of ACM SIGMOD International Conference on Management of Data, 1990.
[MP94] I. S. Mumick and H. Pirahesh. Implementation of magicsets in a relational database system. In Proceedings of ACM SIGMOD International Conference on Management of Data, 1994.
[RLK86] J. Rohmer, R. Lescoeur,and J. M. Kerisit. The Alexander method: A technique for the processing of recursive axioms in deductive databases. In New Generation Computing, 4(3):273--285, 1986.
[RSSS94] R. Ramakrishnan, D. Srivastava, S. Sudarshan and P. Seshadri. The CORAL deductive system. The VLDB Journal, Special Issue on Prototypes of Deductive Database Systems, 1994.
[SAC+79] P. G. Selinger, M. Astrahan, D. Chamberlin, R. Lorie, and T. Price. Access path selection in a relational database management system. In Proceedings of ACM SIGMOD International Conferenceon Managementof Data, 23--34, 1979.
[Sag90] Y. Sagiv. Is there anything better than magic? In Proceedings of the North American Conference on Logic Programming, 235--254, 1990.
[SPL96] P. Seshadri, H. Pirahesh,and T. Y. C. Leung. Decorrelating complex queries. In Proceedings of the Twelfth International Conference on Data Engineering, 1996.
[SS88] S. Sippu and E. SoisalonSoinen. An optimization strategy for recursive queries in logic databases. In Proceedings of the Fourth International Conference on Data Engineering, 1988.
[SS94] P. J. Stuckey and S. Sudarshan. Compiling query constraints. In Proceedingsof the ACM Symposiumon Principles of Database Systems, 1994.
[SSS95] D. Srivastava, P. J. Stuckey and S. Sudarshan. The magic of thetasemijoins. AT&T Bell Laboratories Technical Report, 1995.
[TPCD94] TPC benchmark group. TPCD Draft, December 1994. Information Paradigm. Suite 7, 115 North Wahsatch Avenue, Colorado Springs, CO 80903.
[Yao77] S. B. Yao. Approximating the number of accesses in database organizations. Communications of the ACM, 20(4):260--261, 1977.
6 Заметим, что это условие применимости может всегда удовлетворяться путем выбора в качестве ?2 предиката true.
7 В предположении, что E1 выбирается в качестве первого отношения в порядке сторонней передачи информации.
8 В действительности, при CM-перезаписи используется проекция F на уместные атрибуты, но для простоты изложения мы используем само отношение F. Проекция может быть введена после выполнения шага CMT.
Результаты времени компиляции
На диаграмме на рис. 7 показано общее время компиляции (перезапись + оптимизация) при использовании magopt и nomag. Это время включает второй проход оптимизатора, выполняемый при выборе перезаписи на основе магических множеств (заметим, что в данном случае используется линейная, а не логарифмическая шкала). Для более мелких запросов выбирается перезапись на основе магических множеств, и поэтому время компиляции для magopt почти вдвое больше времени для nomag. Эти накладные расходы представляются нам приемлемыми, поскольку для запросов поддержки принятия решений время компиляции обычно мало по сравнению со временем выполнения.

Рис. 8. Исходные накладные расходы оптимизации
Для более крупных запросов перезапись на основе магических множеств не выбирается и поэтому второй проход оптимизатора отсутствует. Как показывает диаграмма, имеются очень небольшие накладные расходы на анализ целесообразности перезаписи. Это важно в тех случаях, когда накладные расходы на оптимизацию являются существенными. Диаграмма на рис. 8 показывает это более отчетливо; на ней изображено время, затраченное в первом проходе оптимизации, когда magopt анализирует возможность применения Filterjoin. Хотя magopt анализирует большее число планом, в число которых входят планы, включающие Filterjoin, затрачиваемое на это время не очень велико. Этот результат подтверждает наше утверждение о том, что оценочная магическая оптимизация не изменяет порядок сложности оптимизации запросов.
Родственные работы
Перезапись с использованием магических множеств исходно использовалась в области обработки рекурсивных запросов в дедуктивных базах данных [BMSU86, RLK86]. Влияние различных вариантов выбора SIPS обсуждалось в [BR91], и идея использования аппроксимаций магического множества исследовалась в [Sag90, SS88]. Следует заметить, что в данной статье мы имеем дело с нерекурсивными SQL-запросами, поддерживаемыми во всех коммерческих реляционных системах баз данных. Ранее было показано, что магические множества применимы к нерекурсивным SQL-запросам [MFPR90], и соответствующий метод был реализован в системе баз данных Starburst [MP94].
Методы оценочной оптимизации, аналогичные методу магических множеств, могут также применяться к сложным SQL-запросам, включающим корреляцию (с использованием магического преобразования декорреляции [SPL96]) и дорогостоящие функции [Hel95].
При исследовании полусоединений в распределенных базах данных (см., например, [BGW+81, LMH+85]) предполагалось, что отношения являются простыми хранимыми отношениями, и поэтому было легко вычислить стоимость выполнения полусоединений. Кроме того, обычно не рассматривались аспекты, подобные выбору SIPS, поскольку предполагалось, что стоимость коммуникаций перевешивает стоимость локальной обработки (и, следовательно, всегда выбирались наиболее ограничительные полусоединения). Вместо этого оптимизация сосредотачивалась на корректном порядке вычисления полусоединений [BGW+81]. С другой стороны, в проекте System R* [LMH+85] предполагалось, что стоимость локальной обработки перевешивает стоимость коммуникаций; вследствие этого, в процессе оптимизации полусоединения не рассматривались.
В литературе, посвященной неоднородным базам данных, пока еще не рассматривались такие вопросы, как сложные запросы над удаленными представлениями. Однако такие вопросы становятся все более важными, и результаты нашей работы следует применять и в этой области.
CM-преобразования с использованием
?-полусоединения: В следующем правиле преобразования фиксируется базовый шаг CM-перезаписи [SS94]:
где ?2 включает только атрибуты из attrs(F)

Мы называем это преобразование шагом ограничительного магического преобразования (Constraint Magic Transformation, CMT). Шаг CMT может быть порожден из более простых правил преобразования; подробности представлены в [SSS95].
CMT и CM-перезапись:
В выражениях, определяющих E1’ и E2’ в шаге CMT, фиксируется существо CM-перезаписи. Интуитивные соображения состоят в следующем. Предположим, что у нас имеется ограничивающее множество F для результата соединения отношений E1 и E2. При CM-перезаписи этого соединения «фильтрующее» отношение F (также называемое «магическим» отношением) сначала используется для ограничения вычисления E1 кортежами, релевантными F. Затем ограниченный таким образом набор кортежей E1 вместе с фильтрующим отношением F используется для ограничения вычисления E2. Эта стратегия точно фиксируется в шаге CMT.
Более формально, эта связь может быть установлена следующим образом. Рассмотрим представление, определенное как
с фильтрующим отношением F и параметризуемым предикатом ?1 ? ?2, где ?2 включает только атрибуты из attrs(F)
где E1’’ является результатом дополнительной ограничительной магической перезаписи E1 с фильтрующим отношением F и параметризуемым предикатом ?2. Затем представление V заменяется представлением V’, определяемым ниже:
где E2’’ является результатом дополнительной ограничительной магической перезаписи E2 с фильтрующим отношением S1 и параметризуемым предикатом ?1 ? ?3.
Отметим строгое соответствие между E1’ (в CMT) и E1’’ (в ограничительной магии), между правым операндом ?-полусоединения в определении E2’ (в CMT) и S1 (в ограничительной магии) и между E2’ и E1’’. Основное различие между перезаписью ограничительной магией и шагом CMT на одиночном соединении состоит в том, что в CM-перезаписи используются ?-соединения, а не ?-полусоединения. Хотя окончательное выражение, в котором используется ?-полусоединение, является более сложным, чем определение V’, генерируемое при CM-перезаписи, эта дополнительная сложность требуется для сохранения мультимножественной семантики.
Сравниваемые алгоритмы
В своих экспериментах мы сравнивали следующие алгоритмы: отсутствие перезаписи на основе магических множеств (nomag), оценочная оптимизация на основе Filterjoins (magopt) и некоторые возможные «выбранные вручную» предопределенные варианты перезаписи на основе магических множеств (mag1, mag2, mag3, mag4, mag5). Предопределенные варианты представляют некоторые осмысленные варианты выбора SIPS. Для каждого запроса алгоритм magopt должен в оценочной манере выбрать наилучшую SIPS или принять решение о невыполнении перезаписи.
В разд. 2.1 упоминался эвристический подход, изначально предложенный в Starburst [MP94]. При использовании этого подхода запросы сначала оптимизируются без какого-либо использования перезаписи на основе магических множеств, и из результирующего порядка соединений выводятся SIPS. Недостаток этого подхода состоит в том, что при оценивании нигде не вычисляется истинная стоимость магической перезаписи. Путем изучения планов, генерируемых оптимизатором при отсутствии перезаписи на основе магических множеств (nomag), мы cмогли вручную реконструировать поведение подхода Starburst. Мы называем этот алгоритм sbmag.

Рис. 5. Общее сравнение
Упорядочение соединений и SIPS
Разъясним теперь соответствие между перезаписью на основе магических множеств и упорядочением соединений. Рассмотрим исходный запрос на рис. 1. На рис. 1 графически изображены шесть возможных вариантов порядка соединений Emp E, Dept D и DepAvgSal V; предикаты выборки для краткости опущены.

Рис. 4. Некоторые возможные порядки соединений
Сначала рассмотрим планы 1 и 2; результат соединения E и D используется как внешнее отношение в завершающем соединении с представлением V (последнее соединение на рисунке затенено, поскольку эта операция представляет интерес). Как это связано с перезаписью на основе магических множеств? В примере 2 соединение E и D используется как таблица PartialResult, из которой материализуется магическое множество для представления V. Имеется соответствие между составным внешним отношением в плане соединения и таблицей PartialResult, используемой в магической перезаписи. Следовательно, планы 1 и 2 «соответствуют» этому конкретному варианту перезаписи на основе магических множеств. Аналогично, план 3 «соответствует» перезаписи на основе магических множеств, в которой в качестве таблицы PartialResult используется только отношение Dept D. План 4 «соответствует» перезаписи, в которой которой в качестве таблицы PartialResult используется только отношение Emp E. Наконец, планы 5 и 6 «соответствуют» исходному запросу (т.е. перезапись на основе магических множеств не производится).
Мы используем это соответствие для исследования экспоненциального пространство выбора SIPS для перезаписи на основе магических множеств. Мы предлагаем включить анализ вариантов перезаписи на основе магических множеств в оптимизацию соединений путем моделирования магической перезаписи как метода соединения, допуская, тем самым, внедрение нашего подхода в любой оценочный алгоритм оптимизации соединений без существенного изменения кода оптимизатора. Основным изменением оптимизатора является добавление нового метода соединения, и это воздействует на сложность оптимизации только через константный множитель.
Упрощение:
Некоторые преобразования ?-полусоединений могут приводить к генерации выражений, в которых некоторые предикаты проверяются более одного раза; например, в правой части описанного выше преобразования, вводящего ?-полусоединение, предикат ? проверяется дважды. В общем случае повторяющиеся проверки неизбежны, но в некоторых частных случаях они являются избыточными, и выражения можно упростить путем устранения повторяющихся проверок. Следующее преобразование может быть использовано для устранения повторяющихся проверок при наличии возможности его применения.

где attrs(E2) функционально определяют все атрибуты в ?2 над FD(?1)
Заметим, что использование подмножества функциональных зависимостей при выполнении этого преобразования является безопасным, так что полный механизм вывода функциональных зависимостей не существенен.
Устранение
?-полусоединения: Из интуитивных соображений ?-полусоединение можно переписать как соединение, за которым следует проекция, если предикат соединения вместе с функциональными зависимостями правого операнда ?-полусоединения гарантируют, что для каждого кортежа левого операнда выбирается не более одного кортежа левого операнда. Это интуитивное соображение формально фиксируется в следующем правиле преобразования:

где E2.y является суперключом E2, и g(attrs(E1) – это функция от атрибутов E1, возвращающая кортеж той же арности, что и E2.y.
Мы представили характерный образец правил эквивалентности, включающих операцию ?-полусоединения. Более полный набор правил эквивалентности представлен в [SSS95].
Вариации экспериментов
В отдельных экспериментах мы изменяли сложное представление, чтобы оно становилось более дорогим, и повторяли все экспериментальные вариации внешнего блока запроса. Испытывалась также пара вариаций среды выполнения (путем ликвидации некоторых индексов). Результаты оказались очень похожими на приведенные выше, изменялись только абсолютные числа, а не их относительное расположение. По причине ограниченности объема статьи мы не приводим диаграммы результатов. Во всех экспериментах magopt производил выбор, близкий к оптимальному. На основе этого исследования мы заключаем, что метод оптимизации, базирующийся на Filterjoin, является стабильным; его успех не зависит от природы сложного представления, природы блока запроса, в котором используется это представление, а также от наличия индексов.
В современных системах реляционных баз
В современных системах реляционных баз данных обрабатываются сложные SQL-запросы, включающие представления, табличные выражения и подзапросы с агрегатными функциями. Такие запросы становятся все более важными в приложениях поддержки принятия решений (см., например, тестовый набор TPCD [TPCD94]). Метод перезаписи с использованием магических множеств (см., например, [BMSU86, RLK86, BR91, MFPR90, SS94]) был предложен как эвристическое преобразование для оптимизации таких запросов, и этот метод может приводить к серьезным улучшениям эффективности выполнения запросов [MFPR90]. Может быть много возможных вариантов этой перезаписи даже для одиночного запроса, основанных на решениях относительно распространений связываний. Некоторые из этих вариантов могут в действительности ухудшить эффективность. До данной работы не был продемонстрирован алгоритм эффективного выбора варианта в оценочном стиле. В этой статье устраняется важная преграда к внедрению перезаписи на основе магических множеств в коммерческие базы данных.
В статье анализируются два подхода к решению данной проблемы. Первый подход основывается на моделировании перезаписи на основе магических множеств как метода соединения, и он реализован в системе баз данных DB2 C/S V2. Второй подход представляет модель перезаписи на основе магических множеств, основанную на алгебраических преобразованиях. Оба подхода являются взаимнодополнительными и, взятые совместно, позволяют изучать соответствующие практические и теоретические вопросы.
Целью реализации является разработка алгоритма, в котором учитываются ограничения и требования полнофункциональной СУБД. Перезапись на основе магических множеств моделируется как специальный метод соединения, который может быть добавлен к любому существующему оценочному оптимизатору запросов. Выводятся оценочные формулы, позволяющие оптимизатору выбрать наилучший вариант перезаписи и определить, является ли он полезным. Исчерпывающий поиск среди всех вариантов сущетсвенно увеличивает сложность оптимизации запросов.
Чтобы сохранить порядок сложности процесса оптимизации к пространству поиска применяются разумные ограничения. Изучение производительности на основе реализации в DB2 C/S V2 демонстрирует низкие дополнительные накладные расходы и стабильность алгоритма при выполнении основанного на стоимости выбора, что приводит к существенному сокращению времени выполнения запросов. Существенно то, что результаты показывают, что для перезаписи на основе магических множеств требуется оценочный алгоритм (эффективность алгоритмов, основанных на эвристиках, изменяется при изменении статистики данных и оценок стоимости), и что предложенный оценочный алгоритм работает правильно.
Алгебраический подход к перезаписи на основе магических множеств базируется на правилах эквивалентности на мультимножественной реляционной алгебре, затрагивающих операцию ?-полусоединения. Алгебраический подход позволяет правильно определять пространство поиска и может использоваться в оптимизаторе, основанном на правилах (возможно, совместно с эвристиками для ограничения пространства поиска). Мы представляем характерный набор правил эквивалентности и показываем, как эти правила моделируют перезапись на основе магических множеств для не рекурсивных SQL-запросов.
Сначала мы мотивируем проблему с использованием примера.
View Definition
CREATE VIEW DepAvgSal AS (SELECT E.did, AVG(E.sal) AS avgsal FROM Emp E GROUPBY E.did);
Main Query Block
SELECT E.eid, E.sal FROM Emp E, Dept D, DepAvgSal V WHERE E.did = D.did AND E.did = V.did AND E.age < 30 AND D.budget > 100,000 AND E.sal > V.avgsal
Рис. 1. Исходный запрос
View Definitions
CREATE VIEW PartialResult AS (SELECT E.eid, E.sal, E.did FROM Emp E, Dept D WHERE E.did = D.did AND E.age < 30 AND D.budget > 100,000) CREATE VIEW Filter AS (SELECT DISTINCT P.did FROM PartialResult P ); CREATE VIEW LimitedDepAvgSal AS (SELECT F.did, AVG(E.sal) as avgsal FROM Filter F, Emp E WHERE E.did = F.did GROUPBY F.did);
Main Query Block
SELECT P.eid, P.sal FROM PartialResult P, LimitedDepAvgSal V WHERE P.did = V.did AND P.sal > V.avgsal
Рис. 2. Перезапись на основе магических множеств
В данной статье изложены два
В данной статье изложены два основных результата. Во-первых, предложено практическое решение для интеграции алгоритма перезаписи на основе магических множеств в каркас оценочной оптимизации. Это решение гарантирует, что перезапись применяется эффективно и только в тех случаях, когда это полезно. Реализация данного метода оптимизации в DB2 C/S V2 демонстрирует реализуемость предложенного решения. Кроме того, результаты измерения производительности подтверждают то заявление, что магическая перезапись может быть эффективно оптимизирована в оценочном стиле для широкого диапазона запросов без существенного увеличения накладных расходов на оптимизацию. Второй результат состоит в формализации этих идей путем введения мультимножественной алгебраической операции ?-полусоединения. Представлен характерный набор алгебраических эквивалентностей, затрагивающих эту операций, которые могут использоваться для моделирования магической перезаписи. Алгебраическая характеристика отчетливо определяет полное пространство вариантов вычисления. Далее, правила преобразований могут быть использованы в основанном на правилах оптимизаторе для оптимизации сложных запросов в оценочной манере. Хотя эти результаты получены в двух независимых исследованиях, они являются, по существу, взаимодополняющими. Взятые вместе, они затрагивают теорию и практику применения оптимизации на основе перезаписи магических множеств в оценочном стиле.
?-полусоединения и ограничительная магическая перезапись
При использовании магической перезаписи [BR91, MP94, SS94] запросы к базе данных оптимизируются путем определения дополнительных магических (или фильтрующих) отношений, которые используются как фильтры для ограничения вычислений при обработке запроса. Ограничительная магическая перезапись (Constraint Magic rewriting, CM-перезапись) [SS94] является наиболее общим методом магической перезаписи, и мы представляем порождаемое правило преобразования, в котором фиксируется ключевое интуитивное понимание CM-перезаписи для одного отношения. Повторяющееся применение этого правила преобразования к последовательности соединений производит действие, аналогичное CM-перезаписи одноблочного SQL-запроса. В заключение мы указываем эвристику для применения этого метода к SQL-запросам, которые адресуются не только к хранимым отношениям базы данных, но и к представляемым отношениям; эвристика моделирует поведение CM-перезаписи (с полными SIPS слева направо) на таких запросах.
