Оптимизация подвыражений
Если выражение содержит два или более идентичных подвыражения, то вполне достаточно вычислять значение лишь одного из них.
Рассмотрим следующий пример:
if ((a*b)>0x666 && (a*b)<0xDDD) …
Присвоив результат вычисления (a*b) промежуточной переменной, мы сможем избавиться от одной операции умножения, смотрите:
tmp=a*b;
if (tmp>0x666 && tmp<0xDDD) …
Оптимизировать выражения умеют все три рассматриваемых компилятора, но не каждый из них способен распознавать идентичность выражений при их перегруппировке. Вот, например:
if ((a*b)>0x666 && (b*a)<0xDDD) …
Очевидно, что от перестановки множителей произведение не меняется и (a*b) равно (b*a). Компиляторы Microsoft Visual C++ и WATCOM вычислят значение (a*b) лишь однажды, а Borland C++ примет (a*b) и (b*a) за разные
выражения со всеми вытекающими отсюда последствиями.
Оптимизация пролога/эпилога функций
Ранние Си-компиляторы использовали для адресации локальных переменных базовый указатель стека – регистр BP (EBP в 32-разрядном режиме), помещая в начало каждой функции специальный код, называемый прологом. Пролог сохранял текущее содержимое регистра BP (EBP) в стеке и копировал в него указатель вершины стека, хранимый в регистре SP (ESP). Затем, уменьшением значения регистра SP (ESP), выделялась память локальным переменным функции (стек, как известно, растет снизу вверх).
По завершению функции код эпилога вновь "опускал" регистр-указатель вершины стека, освобождая память, занятую локальными переменными, и восстанавливал значение базового указателя стека – регистра BP (EBP).
Ну, резервирование/освобождение памяти – это понятно, но вот регистр BP (EBP) зачем? А вот зачем: он хранит указатель кадра стека – региона памяти, отведенного под локальные переменные.
Все три рассматриваемых компилятора адресуют локальные переменные иначе – непосредственно через ESP. Это значительно усложняет реализацию компилятора, т.к. указатель вершины стека меняется в ходе выполнения программы и адресация выходит "плавающей", зато такая техника высвобождает один регистр для регистровых переменных и избавляется от двух операций обращения к памяти (сохранения/восстановления EBP), что заметно повышает производительность.
__встраиваемые функции
__отложенное выталалкивание аргументов из стека
Оптимизация работы с памятью
Эта глава посвящена вопросам оптимизации обработки больших массивов данных и потоковых алгоритмов, – всем тем ситуациям, когда интенсивный обмен с памятью неизбежен. (Обработка компактных структур данных с многократным обращением к каждой ячейки – тема отдельного разговора, подробно рассмотренная в главе "Оптимизация обращения к памяти и кэшу").
Несмотря на стремительный рост своей пропускной способности и значительное сокращение времени доступа,– оперативная память по-прежнему остается одним из узких мест, сдерживающих производительность всей системы. Тем более обидно, что в силу архитектурных особенностей платформы IBM PC, теоретическая (она же – заявленная) пропускная способность практически никогда не достигается.
Типовые алгоритмы обработки данных задействуют быстродействие оперативной памяти едва ли на треть, а зачастую намного менее того! Удивительно, но большинство программистов даже не подозревают об этой проблеме! Одно из возможных объяснений этого феномена заключается в том, что мало кто измеряет производительность своих программ в мегабайтах обработанной памяти в секунду (а если и измеряет, то списывает низкую пропускную способность на громоздкость вычислений, хотя время, потраченное на вычисления, в данном случае играет второстепенную роль).
Грамотно организованный обмен данными выполняется как правило в три-четыре раза быстрее, причем (и это замечательно!) эффективное взаимодействие с памятью достижимо на любом языке (в том числе и интерпретируемом!), а не ограничено одним лишь ассемблером.
Вопреки возможным опасением читателей, предложенные автором приемы оптимизации аппаратно независимы и успешно работают на любой платформе под любой операционной системой. Вообще-то, в каком-то высшем смысле, все обстоит не совсем так и выигрыш в производительности достигается исключительно за счет учета конкретных конструктивных особенностей конкретной аппаратуры, ? бесплатного хлеба, увы, не бывает. Тем не менее, на счет переносимости автор не так уж и соврал, – подавляющее большинство современных систем построено на базе DRAM и принципы работы с различными моделями динамической памяти достаточно схожи. Во всяком случае, в ближайшие несколько лет никаких революций в этой области ожидать не приходится.
Что касается же DDR- и Rambus DRAM памяти, – техника оптимизации под нее придерживается полной преемственности, и дает весьма значительный прирост производительности, намного больший, чем в случае с "обычной" SDAM. Нужно ли лучшее подтверждение переносимости предложенных алгоритмов?
Оптимизация распределения переменных
В языках Си/Си++ существует ключевое слово "register", предназначенное для принудительного размещения переменных в регистрах. И все бы было хорошо, да подавляющее большинство компиляторов втихую игнорируют предписания программистов, размещая переменные там, где, по мнению компилятора, им будет "удобно". Разработчики компиляторов объясняют это тем, что компилятор лучше "знает" как построить наиболее эффективный код. "Не надо", – говорят они, "пытаться помочь ему". Напрашивается следующая аналогия: пассажир говорит – "мне надо в аэропорт", а таксист без возражений едет "куда удобнее".
Ну, не должна работа на компиляторе превращаться в войну с ним, ну никак не должна! Отказ разместить переменную в регистре вполне законен, но в таком случае компиляция должна быть прекращена с выдачей сообщения об ошибке, типа "убери register, а то компилить не буду!", или на худой конец – выводе предупреждения.
Впрочем, ладно, все это лирика. Гораздо интереснее вопрос – какую именно стратегию распределения переменных по регистрам использует каждый компилятор.
Компиляторы Borland C++ и WATCOM при нехватке регистров помещают в них наиболее интенсивно используемые перемеренные, а все остальные "поселяют" в медленной оперативной памяти. Компилятор же Microsoft Visual C++ не учитывает частоты использования переменных и размещает их в регистрах в порядке объявления.
__освобождение переменных
Оптимизация штатных Си-функций для работы с памятью
Штатные библиотеки языка Си включают в себя большое количество функций, ориентированных на работу с блоками памяти. К ним, в частности, относятся: memcpy, memmove, memcmp, memset и др. В подавляющем большинстве случаях эти функции реализованы на ассемблере и достаточно качественно оптимизированы. Тем не менее, резерв производительности еще есть и путем определенных ухищрений можно сократить время обработки больших блоков памяти чуть ли не в несколько раз! Начнем?..
Оптимизация memcpy. Большинство реализаций функции memcpy выглядят приблизительно так: "while (count--) *dst++ = *src++". Этот код имеет по крайней мере три проблемы: перекрытие транзакций чтения/записи, невысокую степень параллелизма обработки ячеек и возможность пересечения обоих потоках в одном и том же DRAM-банке.
Перекрытие транзакций чтения/записи устраняется блочным копированием памяти через кэш-буфер: пусть один цикл считывает несколько килобайт источника в кэш, а другой цикл записывает содержимое буфера в приемник. В результате вместо чередования транзакций чтение – запись – чтение – запись… мы получаем две раздельных серии транзакций: чтение ? чтение ? чтение… и запись – запись – запись... Некоторое перекрытие транзакций на границах циклов все же останется, но если размер буфера составляет хотя бы 1 Кб этими издержками можно полностью пренебречь.
Параллелизм загрузки данных легко усилить, если обращаться к ячейкам с шагом равным размеру пакетного цикла чтения (см. "Параллельная обработка данных"). Для простоты можно остановится на шаге в 32 байта, но в критичных к быстродействию приложениях, оптимизируемых под процессоры старшего поколения (AMD Athlon, Pentium?4), эту величину рекомендуется определять автоматически или задавать опционально.
Пагубное влияние возможного пересечения потоков данных в одном DRAM-банке в данной схеме исчезает само собой, поскольку потоки обрабатываются последовательно, а не параллельно.
Образно выражаясь, можно сказать, что одним выстрелом мы убиваем сразу трех (!) зайцев, – копирование памяти через промежуточный буфер ликвидирует все слабые стороны алгоритма штатной функции memcpy, значительно увеличивая тем самым ее производительность.
Улучшенный вариант реализации memcpy может выглядеть, например, следующим образом:
for (a = 0; a < count; a += subBLOCK_SIZE)
{
for(b = 0; b < subBLOCK_SIZE; b += BRUST_LEN)
tmp += *(int *)((int)src + a + b);
memcpy((int*)((int)dst + a ),(int*)((int)src + a), subBLOCK_SIZE);
}
Листинг
29 [Memory/memcpy.optimize.c] Оптимизированная реализация memcpy
На AMD Athlon 1050/100/100/VIA KT133 оптимизированный вариант memcpy выполняется практически на треть быстрее и это очень хорошо! Правда, на P?III/733/133/100/I815EP прирост производительности намного меньше и составляет всего лишь ~10%. Увы, устраняя одни проблемы, мы неизбежно создаем другие. Предложенный способ оптимизации memcpy имеет как минимум два серьезных недостатка. Во-первых, увеличение количества циклов с одного до трех несет значительные накладные расходы, которых никакими ухищрениями невозможно избежать. Во-вторых, цикл, загружающий данные из оперативной памяти в кэш, фактически работает вхолостую, – запихивая полученные ячейки в неиспользуемую переменную, в то время как цикл, записывающий данные в память, вынужден повторно
обращаться к уже загруженным ячейкам. Т.е. count/BRUST_LEN ячеек копируются как бы дважды. К сожалению, первый цикл не может непосредственно записывать полученные ячейки в память, поскольку это неизбежно вызовет перекрытие шинных транзакций и лишь ухудшит производительность.
Ассемблерная реализация данного алгоритма, конечно, увеличит его быстродействие, но не намного. Гораздо лучший результат дает использование предвыборки (см. "Кэш. Предвыборка"), но это уже тем другого разговора.
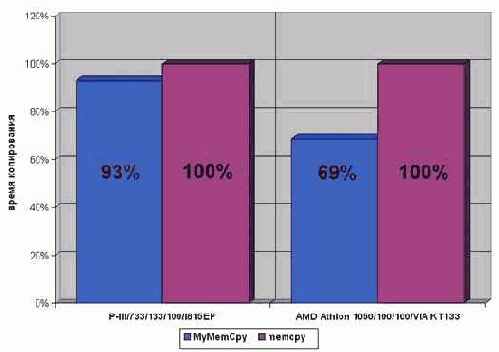
Рисунок 43 graph 0x021 Демонстрация эффективности параллельного копирования памяти.
Выигрыш особенно ощутим на процессорах Athlon – целых ~30% производительности
Оптимизация memmove Функция memmove, входящая в стандартную библиотеку языка Си, выгодно отличается от своей ближайшей родственницы memcpy тем, что умеет копировать перекрывающиеся блоки памяти. За счет чего это достигается? Если адрес приемника расположен "левее" источника (т.е. лежит в младших адресах) алгоритм копирования реализуется аналогично memcpy, поскольку ячейки памяти переносятся "назад", – в свободную неинициализированную область (см. рис 37 сверху). Единственное условие – количество ячеек памяти, переносимых за одну итерацию, не должно превышать разницу адресов приемника и источника. То есть, если приемник расположен всего в двух байтах от источника, переносить памяти двойными словами уже не получится!
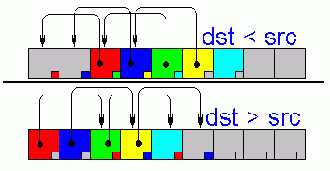
Рисунок 44 0х37 Копирование перекрывающихся блоков памяти. Если источник расположен правее приемника (верхний рисунок), то перенос ячеек памяти происходит без каких-либо проблем. Напротив, если источник расположен левее приемника (нижний рисунок), то перенос ячеек "вперед" приведет к затиранию источника
Гораздо сложнее справится с ситуацией, когда приемник расположен правее источника (т.е. лежит в старших адресах). Попытка скопировать память слева направо приведет к краху, т.к. перенос ячеек будет осуществляться в уже "занятые" адреса с неизбежным затиранием их содержимого. Попросту говоря, memcpy в этом случае будет работать как memset (см. рис. 37 снизу), что явно не входит в наши планы. Как же выйти из этой ситуации? Обратившись к исходным текстам функции memmove (в частности у Microsoft Visual C++ они расположены в каталоге \Microsoft Visual Studio\VC98\CRT\SRC\memmove.c), мы обнаружим следующий подход:
/*
* Overlapping Buffers
* copy from higher addresses to lower addresses
*/
dst = (char *)dst + count - 1;
src = (char *)src + count - 1;
while (count--) {
*(char *)dst = *(char *)src;
dst = (char *)dst - 1;
src = (char *)src - 1;
}
Листинг 30 Пример реализации функции memmove в компиляторе Microsoft Visual C++
Ага, память копируется с зада наперед, т.е. справа налево. В таком случае затирания ячеек гарантированно не происходит, но… за это приходится платить. Ведь ## как мы уже знаем, подсистема памяти оптимизирована именно под прямое чтение, и попытка погладить ее "против шерсти" ничего хорошего в плане быстродействия не несет. Насколько сильно это снижает производительность? На этот вопрос нет универсального ответа. В зависимости от особенностей архитектуры используемого аппаратного обеспечения эта величина может колебаться в несколько раз.
В частности, на Intel P-III/Intel 815EP обратное копирование памяти уступает прямому приблизительно в полтора раза. А вот на AMD Athlon/VIA KT133 разница в скорости между прямым и обратным копированием составляет всего ~2%, чем со спокойной совестью можно пренебречь. Тем не менее, компьютеры на основе Athlon/KT133 занимают значительно меньшую долю рынка, нежели системы на базе Intel Pentium, поэтому не стоит закладываться на такую конфигурацию.
При интенсивном использовании memmove общее снижение производительности может оказаться весьма значительным и неудивительно, если у разработчика возникнет жгучее желание ну хоть немного его поднять. Это действительно возможно сделать, достаточно лишь копировать память не байтами и даже не двойными словами, а… блоками с размером равным разнице адресов приемника и источника. Если размер блока составит хотя бы пару килобайт, память будет копироваться в прямом направлении, хотя и задом наперед. Как это можно реализовать на практике? Рассмотрим следующий пример, написанный на чистом Си без применения ассемблера. Для повышения наглядности отсюда исключен вспомогательный код, обеспечивающий, в частности, обработку ошибок и выравнивание стартовых адресов с последующим переносом "хвоста" (см. "Выравнивание данных").
int __MyMemMoveX(char *dst, char *src, int size)
{
char *p1,*p2;
int a,x=1;
int delta;
delta=dst-src;
if ((delta<1)) return -1;
for(a=size;a>delta;a-=delta)
memcpy(dst+a-delta,src+a-delta,delta);
return 0;
}
Листинг 31 Оптимизированный вариант реализации memmove, копирующий память блоками в прямом направлении, хотя и задом на перед
В сравнении со штатной memmove данная функция работает на 20% быстрее (если разница адресов источника и приемника не превышает размер кэш-памяти первого уровня) и на 30% при перемещении блоков памяти на большое расстояние (см. graph 15). Причем, это еще не предел, – переписав функцию MyMemMoveX на ассемблер, мы получим еще больший прирост производительности (см. так же "Параллельная обработка данных", "Кэш. Предвыборка").
Разумеется, если разница адресов источника и приемника невелика (менее килобайта), то "обмануть" систему не получится, и память будет копироваться скорее в обратном направлении, чем в прямом. При этом, накладные расходы на организацию цикла поблочного копирования вызовут значительное снижение производительности, проигрывая штатной memmove в два и более раз. Поэтому, на область применения MyMemMoveX наложены определенные ограничения.
Хорошо, но ведь бывают же такие случаи, когда перекрывающиеся области необходимо копировать именно "вперед"? Допустим, у нас имеется поток данных, не поддерживающий позиционирование указателя или, скажем, весь блок памяти на момент начала копирования целиком еще недоступен. Вот вполне жизненный пример (из практики автора) – при перемещении фрагментов изображения в графическом редакторе техническое задание требовало выполнять обновление изображения от начала блока к концу. (Дабы пользователь мог приступать к работе с изображением, не дожидаясь, пока блок будет перемещен целиком). Причем, использовать ссылочную организацию данных запрещалось. (Кто сказал, что это глупость? нет, это не глупость, это ? техническое задание).
Тупик? Вовсе нет! Напротив, – возможность поразмять мозги ( ну не все же время рисовать интерфейсы в Visual Studio).
Первое, что приходит на ум, – перенос памяти через промежуточный буфер. Все идея реализуется тривиальным кодом вида:
mymovemem(char *dst, char *src, int size)
{
char *tmp;
tmp=malloc(BLOCK_SIZE);
memcpy(tmp, src, BLOCK_SIZE);
memcpy(dst, tmp, BLOCK_SIZE);
}
Листинг 32 Вариант реализации memmove с переносом памяти через промежуточный буфер
Гуд? Да какой там гуд!!! Во-первых, предложенный алгоритм удваивает
количество потребляемой памяти, что в ряде случаев просто неприемлемо; во-вторых, он в два раза увеличивает время копирования и, наконец, в-третьих, он не решает задачи, поставленной в ТЗ. Ведь обновление начала изображения начнется не сразу, а через довольно продолжительное время, в течение которого будет заполняться временный буфер. Так что не стоит этот алгоритм и обсуждать!
Но, постойте, зачем нам копировать весь перемещаемый блок в промежуточный буфер целиком? Достаточно сохранить лишь ту его часть, которая затирается выступающим влево "хвостом". Т.е. максимально разумный размер буфера равен dst – src. Рассмотрим упрощенный вариант алгоритма прямого перемещения памяти, использующий два таких буфера. Назовем его четырехтактным потоковым алгоритмом копирования памяти. Почему "четырехтактным" станет ясно ниже.
Итак, такт первый. memcpy(BUF_1, dst, dst - src)
– мы сохраняем память приемника, поскольку, этот фрагмент будет затерт в следующем такте (см. рис. 36).
Такт второй: memcpy(dst, src, dst - src)
– мы копируем (dst – src) байт из источника в приемник, не беспокоясь о затираемой памяти, т.к. она уже сохранена в буфере.
Такт третий: memcpy(BUF_2, dst + (dst – src), dst – src) – сохраняем следующую порцию данных приемника во втором промежуточном буфере.
Такт четвертый: memcpy(dst+ (dst – src), BUF_1, dst – src) – "выливаем" содержимое буфера BUF_1 на положенное место (оно только что было сохранено в BUF_2).
Все! Первый буфер освобождается и можно смело переходить к такту I, – "рабочий цикл" нашего "движка" завершен.
Как нетрудно убедиться, копирование происходит только в прямом направлении, причем память приемника обновляется от начала к концу маленькими порциями по (dst – src) байт. (При "мышином" перетаскивании областей изображений в графическом редакторе они, действительно, недалеко уползают за один шаг; кстати, Microsoft Paint (графический редактор из штатной поставки Windows) при перетаскивании изображений перемещает память именно memmove, поэтому жутко тормозит даже на P-III).
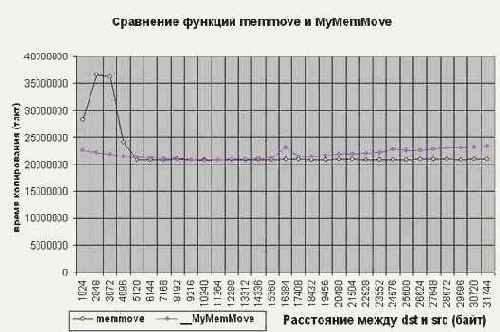
Причем, если разница адресов источника и приемника составляет порядка 4-8 Кб, то, несмотря на двойной перегон памяти к буферам и обратно, предложенный алгоритм даже обгоняет
memmove на 10%, – во всяком случае на P-III (см. рис. graph 18). А на AMD Athlon/VIA KT133 разница достигает аж 1,7 крат (в пользу нашего алгоритма, естественно), впрочем, это отнюдь не показатель крутости алгоритма, – просто VIA KT133 так уж устроен.
А теперь давайте подумаем: можно ли уменьшить количество буферов с двух до одного? Разумеется, да, – ведь на момент завершения второго такта, регион [src[0]…src[dst-src]] (на рис. 36 он закрашен красным цветом) уже свободен и может использоваться для временного хранения данных. Однако тут есть один подводный камень, – если адреса "своих" временных буферов мы можем выбирать самостоятельно с учетом архитектуры и организации DRAM, то адрес источника нам дается "извне" со всеми отсюда вытекающими… Разумеется, ничего невозможно нет и при желании обойтись всего одним буфером при не сильно худшей эффективности – вполне возможно, но это значительно усложнит алгоритм и снизит его наглядность. А алгоритм, надобно сказать, и без того не слишком прозрачен (см. листинг…MyMemMove)
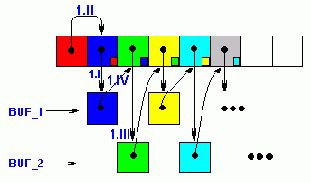
Рисунок 45 0x036 "Четырехтактный" алгоритм прямого переноса памяти с использованием двух промежуточных буферов
#define BUF_SIZE 256*K
int __MyMemMove(char *dst, char *src, int size)
{
char BUF_1[BUF_SIZE];
char BUF_2[BUF_SIZE];
char *p1, *p2;
int a,x = 1;
int delta;
delta=dst-src;
if ((delta>BUF_SIZE) || (delta<1)) return -1;
p1 = BUF_1;
p2 = src;
for(a = 0; a<size/delta; a++)
{
memcpy(p1,dst,delta);
memcpy(dst,p2,delta);
if (x)
{
p1 = BUF_2; p2 = BUF_1;
x =
0;
}
else
{
p1 = BUF_1; p2 = BUF_1;
x =
1;
}
dst +=
delta;
}
return 0;
}
Листинг 33 Вариант реализации четырехтактного алгоритма переноса памяти только в прямом направлении с использованием двух промежуточных буферов
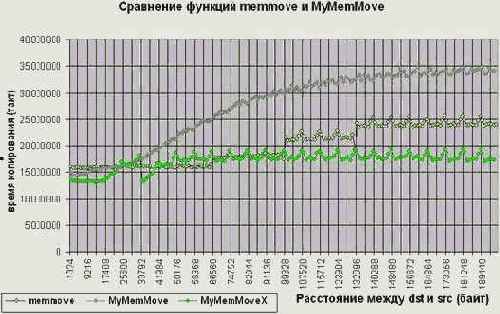
Рисунок 46 graph 15 Демонстрация эффективности различных алгоритмов переноса памяти
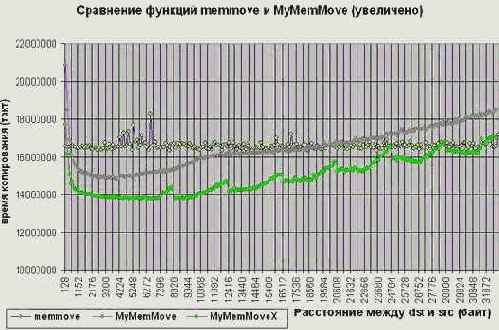
Рисунок 47 graph 18 Демонстрация эффективности различных алгоритмов переноса памяти (увеличено)
Рисунок
48 graph 16 Сравнение функций memmove и MyMemMove на системе AMD Athlon 1050/100/100/VIA KT133
Оптимизация функции memcmp
Несмотря на то, что функция memcmp не относится к числу самых популярных (так, в MSDN memcpy упоминается 500 раз, а memcmp и memmove – всего 150 и 50 раз соответственно) это еще не дает оснований пренебрегать качеством ее реализации. Начнем с анализа штатных библиотек вашего компилятора. В большинстве случаев сравнение блоков памяти осуществляется приблизительно так:
void * __cdecl _memccpy (void * dest, const void * src, int c, unsigned count)
{
while ( count && (*((char *)(dest = (char *)dest + 1) - 1) =
*((char *)(src = (char *)src + 1) - 1)) != (char)c ) count--;
return(count ? dest : NULL);
}
Листинг 34 Реализация memcmp в компиляторе Microsoft Visual C++ 6.0
Фи! Тормозное побайтное сравнение безо всяких попыток оптимизации! Правда в комплект поставки Visual C++ входит и ассемблерная реализация той же самой функции (ищите ее в каталоге \SRC\Intel). Ну-ка, посмотрим, что там (по соображениям экономии места исходный текст не приводится): ага, если оба указателя кратны четырем, сравнение ведется двойными словами (что намного быстрее) и лишь в противном случае – по байтам. Гуд? А вот и не гуд! Кратность начальных адресов – условие вовсе необязательное для 32-разрядного сравнения (строго говоря, процессоры серии 80x86 вообще не требуют осуществлять выравнивания, просто небрежное отношение с не выровненными адресами может несколько снизить быстродействие – подробнее см. "Выравнивание адресов"). Если три младших бита обоих указателей равны, функция может выровнять их и самостоятельно, просто сместившись на один, два или три байта "вперед".
Впрочем, эти рассуждения все равно беспредметны, поскольку, в режиме оптимизации по скорости (ключ "/O2") Microsoft Visual C++ отказывается от использования ряда библиотечных функций и заменяет их intrinsic-ами (см. "pragma intrinsic" в документации по компилятору). Забавно, но разработчики компилятора, по-видимому, сочли, что выполнять множество проверок и "тянуть" за собой несколько вариантов реализации функции сравнения будет нерационально (?) и потому они ограничились одним универсальным решением – тривиальным побайтовым сравнением. Неудивительно, что после такой "оптимизации" быстродействие memcmp значительно ухудшилось.
Чтобы запретить компилятору самовольничать, – используйте прагму "function" с указанием имени функции, например, так: "#pragma function(memcmp)". В частности, на P-III это ускорит выполнение функции приблизительно на 36%! Правда, на Athlon разница в производительности будет существо меньше – порядка 10%. Кстати, в защиту Microsoft можно сказать, что ее реализация memcmp на 20%-30% быстрее, чем у Borland C++ 5.5.
Но и это еще не предел!
Для memcmp (как и для большинства остальных функций, работающих с памятью) актуальна проблема оптимального чередования DRAM-банков (см. "Стратегия распределения данных по DRAM-банкам"). Если оба сравниваемых блока начинаются с различных страниц одного и того же банка, время доступа к памяти существенно замедляется. Поэтому, мы должны уметь отслеживать такую ситуацию, при необходимости увеличивая один из указателей на длину DRAM-страницы. Это повысит скорость выполнения функции приблизительно на 40% на P-III и на целых 60%-70% на AMD Athlon (да-да, практически в три раза!). Правда, тут есть одно "но". Память должна обрабатываться не байтами, а двойными словами, в противном случае прирост производительности составит всего лишь 5% для P-III и немногим менее 30% для AMD Athlon.
Хорошо, а если адреса сравниваемых блоков к нам поступают "извне" и скорректировать их невозможно? Существует два пути: смириться с низкой производительностью или… сравнивать не сами блоки памяти, а их контрольную сумму. Конечно, теоретически не исключено, что контрольные суммы различных блоков памяти "волшебным" образом совпадут, но в подавляющем большинстве случаев эта вероятность настолько мала, что ей вполне можно пренебречь. К тому же, считать контрольную сумму всего блока абсолютно необязательно – достаточно ограничиться одной DRAM-страницей (можно в принципе и меньшей величиной, главное, чтобы переключения между страницами одного банка происходили не слишком часто). За счет сокращения количества параллельно обрабатываемых потоков данных с двух до одного, хеш-алгоритм работает намного быстрее штатной функции сравнения памяти, обгоняя ее на ~35% и ~55% на P-III и AMD Athlon соответственно. Правда, при оптимальном чередовании банков памяти, хеш-алгоритм все же проигрывает функции, сравнивающей память двойными словами. Причем, если на P-III хеш-алгоритм отстает от нее всего на 1%, то на AMD Athlon разрыв в производительности достигает целых 10%!
Таким образом, хеш-алгоритм целесообразно использовать только
при неоптимальном чередовании DRAM-банков. Впрочем, категоричность этого утверждения смягчает одна оговорка. Если мы сократим длину хешируемого блока до величины пакетного цикла обмена, на P-III мы получим практически 60% выигрыш в производительности, обогнав самый быстрый алгоритм двойных слов более чем на 20%! Ценой же за это станет постоянное переключение DRAM-страниц и, как следствие, потеря возможности противостоять неблагоприятному чередованию банков памяти. Однако такой значительный прирост скорости стоит того! Увы, этот эффект имеет место лишь на Intel и не переносим на AMD/VIA. С другой стороны, Pentium?ам принадлежит более половины компьютерного рынка и оснований для отказа от предложенного трюка, в общем-то, нет. Тем более что даже на AMD Athlon он (хеш-алгоритм) работает значительно быстрее штатной функции сравнения памяти. Один из возможных вариантов его реализации будет выглядеть так:
for(a=0;a<BLOCK_SIZE;a+=DRAM_PG_SIZE)
{
crc_1=0; crc_2=0;
for(b = 0; b < DRAM_PG_SIZE; b += sizeof(int))
// Внимание! Это очень слабый алгоритм подсчета CRC
// и его можно использовать _только_ для демонстрации
crc_1 += *(int*)((int)p1+a+b);
for(b = 0; b < DRAM_PG_SIZE; b += sizeof(int))
crc_2 += *(int*)((int)p2+a+b);
if (crc_1 != crc_2)
break; // Если CRC не совпадают, следовательно,
// блоки памяти различны.
// При необходимости можно вызвать
// memcmp(p1+a, p2+a, BLOCK_SIZE-a)
// для уточнения результата
}
Листинг 35 Оптимизированный вариант реализации memcmp с использованием хеш-алгоритма
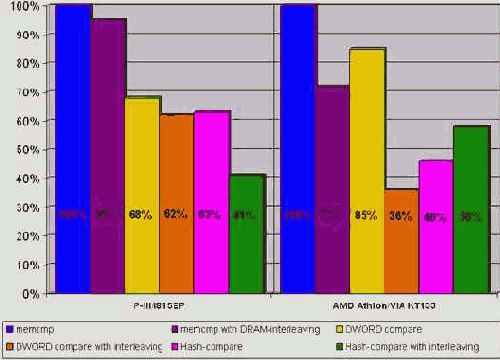
Рисунок 49 graph 19 Демонстрация эффективности различных алгоритмов сравнения блоков памяти.
Оптимизация memset. Нет никаких идей по поводу оптимизации данной функции.
Особое замечание по функциями Win32 API В win32 API входит множество функций для работы с блоками памяти, среди которых присутствуют и прямые эквиваленты штатных функций языка Си: CopyMemory (эквивалент memcpy), MoveMemory (эквивалент memmove) и FillMemory
(эквивалент memset).
Возникает вопрос: чем лучше пользоваться – функциями операционной системы или функциями самого языка? Ответ: компания Microsoft намеренно заблокировала возможность использования функций ядра операционной системы, включив в заголовочные файлы WINBASE.H и WINNT.H следующий код:
#define MoveMemory RtlMoveMemory
#define CopyMemory RtlCopyMemory
#define FillMemory RtlFillMemory
#define ZeroMemory RtlZeroMemory
Листинг 36 Фрагмент WINBASE.H
#define RtlEqualMemory(Destination,Source,Length)
(!memcmp((Destination),(Source),(Length)))
#define RtlMoveMemory(Destination,Source,Length)
memmove((Destination),(Source),(Length))
#define RtlCopyMemory(Destination,Source,Length)
memcpy((Destination),(Source),(Length))
#define RtlFillMemory(Destination,Length,Fill)
memset((Destination),(Fill),(Length))
#define RtlZeroMemory(Destination,Length)
memset((Destination),0,(Length))
Листинг 37 Фрагмент WINNT.H
Вот это номер! Оказывается, функции семейства xxxMemory представляют собой макро-переходники к штатным функциям языка! Причем, это отнюдь не корпоративная тайна, а вполне документированная особенность, косвенно подтверждаемая Platform SDK. При внимательном изучении описания функции MoveMemory мы обнаружим следующее:
Quick Info
Windows NT: Requires version 3.1 or later.
Windows: Requires Windows 95 or later.
Windows CE: Unsupported.
Header: Declared in winbase.h.
Ну и что здесь особенного? А вот что: строка "Import Library" отсутствует! Следовательно, функция MoveMemory целиком реализована во включаемом файле WINBASE.H, о чем Microsoft нас и предупреждает.
Но это еще не конец истории. Скорее, только ее начало.
Давайте, воспользовавшись утилитой DUMBDIN, посмотрим на список функций, экспортируемых "ядреной" библиотекой операционной системы – файлом KERNEL32.DLL. Вопреки логике и здравому смыслу мы обнаружим следующее:
598 255 RtlFillMemory (forwarded to NTDLL.RtlFillMemory)
599 256 RtlMoveMemory (forwarded to NTDLL.RtlMoveMemory)
600 257 RtlUnwind (forwarded to NTDLL.RtlUnwind)
601 258 RtlZeroMemory (forwarded to NTDLL.RtlZeroMemory)
Выходит, что функции RtlMoveMemory, RtlFillMemory и RtlZeroMemory в ядре системы все-таки есть! Причем, это не просто "заглушки", все тело которых состоит из одного оператора return, а вполне работоспособные функции. Чтобы убедиться в этом, достаточно вызвать любую из функций напрямую в обход SDK. Одина из возможных реализаций приведена ниже (обработка ошибок по соображениям наглядности не приведена):
HINSTANCE h;
#undef RtlMoveMemory
void (__stdcall *RtlMoveMemory)(void *dst, void* src, int count);
h=LoadLibrary("KERNEL32.DLL");
RtlMoveMemory = (void (__stdcall *)(void *dst, void* src, int count))
GetProcAddress(h, "RtlMoveMemory");
Листинг 38 Пример вызова RtlMoveMemory явной компоновкой
Впрочем, использовать RtlMoveMemory вместо memmove, – не очень хорошая идея и Microsoft не зря заблокировала ее вызов. Функция RtlMoveMemory совершенно отвратительно оптимизирована. Во-первых, она не выравнивает адреса перемещаемых блоков памяти, а, во?вторых, перекрывающиеся блоки памяти в случае src < dst копирует по байтам, что нельзя признать оптимальным.
На платформе P-III/733/133/100/I815EP функция RtlMoveMemory проигрывает штатной функции memmove компилятора Microsoft Visual C++ 6.0 чуть ли не в полтора раза! Правда, на AMD Athlon 1050/100/100/VIA KT133 ситуация диаметрально противоположная, – здесь функция memmove отстает от своей конкурентки, причем весьма значительно, – на целых ~30%!
С функцией FillMemory ситуация более постоянна. На всех системах она показывает ничуть не худший результат, чем штатная функция языка memset и потому совершенно все равно какую из них использовать. Аналогичная картина наблюдается и с функцией ZeroMemory, являющиеся прямой родственной FillMemory, но заполняющий блок памяти нулями, а не произвольным значением. С другой стороны, с практической точки зрения "FillMemory" на целых три символа длиннее, чем "memset" и потому использование последней все же предпочтительнее. Впрочем, эта оценка достаточна субъективна. Встречаются эстеты, которые находят, что "FillMemory" выглядит красивее, чем "memset" и к тому же намного легче читается. Что ж, выбирайте то, что вам больше по душе!
Может показаться, что при инициализации множества крошечных блоков памяти использование FillMemory повлечет за собой значительные накладные расходы на многократный вызов функции. (memset в отличие от нее может быть непосредственно вживлена в исполняемый код как inline, – обычно она и вживляется). На самом же деле, современные процессоры так быстры, что временем вызова функции можно полностью пренебречь. Разница в производительности memset и FillMemory едва ли превысит несколько процентов, что практически не скажется на общем быстродействии программы.
Вы, наверное уже обратите внимание, что в списке win32 API функций отсутствует какой бы то ни было аналог memcmp. Это действительно странно, поскольку в файле WINNT.H такая функция все-таки есть:
#define RtlEqualMemory(Destination,Source,Length)
(!memcmp((Destination),(Source),(Length)))
А в среди функций, экспортируемых NTDLL.DLL есть RtlCompareMemory, которая, как нетрудно догадаться из нее названия, именно та, которая нам и нужна! Причем, в отличие от функции RtlMoveMemory, функция сравнения памяти достаточно прилично оптимизирована и даже обгоняет штатную функцию memcmp компилятора Microsoft Visual C++ 6.0 (см.
рис. graph 23). На P-III/733/133/I815EP разрыв в производительности составляет ~40%, а на AMD Athlon 1050/100/100/VIA KT133 – ~15%.
К сожалению, функция RtlCompareMemory не реализована на Windows 9x и программа, ее использующая, будет работать только под NT/W2K. Конечно, можно распространять свой продукт вместе с библиотекой NTDLL.DLL, позаимствованной, из каталога WINNT\SYSTEM (только переименуйте ее во что ни будь другое, т.к. в Win9x уже есть "своя" NTDLL.DLL), но не проще ли самостоятельно реализовать memcmp, тем более, что в этом нет ничего сложного? "Изюминка" функции RtlCompareMemory заключается в том, что в отличие от memcmp она сравнивает память не байтами, а двойными словами. Вот и весь секрет ее производительности!
Заключительный вердикт: при разработке критичных к быстродействию приложений лучше всего использовать собственные реализации функций, работающих с памятью, оптимизированных с учетом рекомендаций, приводимых в данной главе. И штатные функции языка, и функции операционной системы в той или иной степени не оптимальны.
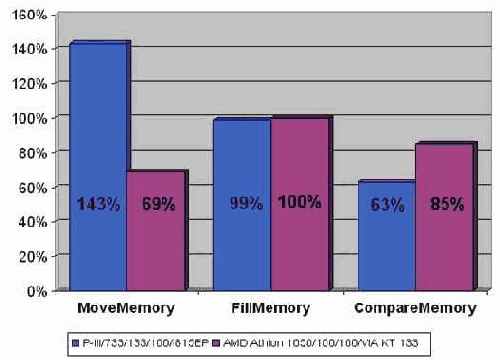
Рисунок 50 graph 23 Сравнительная характеристика шатанных функций компилятора Microsoft Visual C++ и эквивалентных им функций операционной системы. Кстати, все они в той или иной степени не оптимальны
Оптимизация сортировки больших массивов данных
"По оценкам производителей компьютеров в 60-х годах в среднем более четверти машинного времени тратилось на сортировку. Во многих вычислительных системах на нее уходит больше половины машинного времени…" Дональд Э. Кнут "Искусство программирования. Том 3. Сортировка и поиск".
…прошло полвека. Процессорные мощности за это время необычайно возросли, но ситуация с сортировкой навряд ли значительно улучшилось. Так, на AMD Athlon 1050 MHz упорядочивание миллиона чисел одним из лучших алгоритмов сортировки – quick sort – занимает 3,6 сек., а десяти миллионов – уже свыше пяти минут (см. рис. graph 33). Сортировка сотен миллионов чисел вообще требует астрономических количеств времени. И это при том, что сортировка – она из наиболее распространенных операций, встречающееся буквально повсюду. Конечно, потребность в сортировке сотен миллионов чисел есть разве что у ученых, моделирующих движения звезд в галактиках или расшифровывающих геном, но ведь и в бизнес приложениях таблицы данных с сотнями тысяч записей – не редкость! Причем, к производительности интерактивных приложений предъявляются весьма жесткие требования, – крайне желательно, чтобы обновление ячеек таблицы происходило параллельно с работой пользователя, т.е. осуществлялась налету.
Алгоритму быстрой сортировки требуется O(n lg n) операций в среднем и O(n2) в худшем случае. Это действительно очень быстрый алгоритм, который навряд ли можно значительно улучшить. Действительно, нельзя. Но надо! Вспомните Понедельник Стругакцих: "Мы сами знаем, что она [задача] не имеет решения, - сказал Хунта, немедленно ощетинившись. – Мы хотим знать, как ее решать"
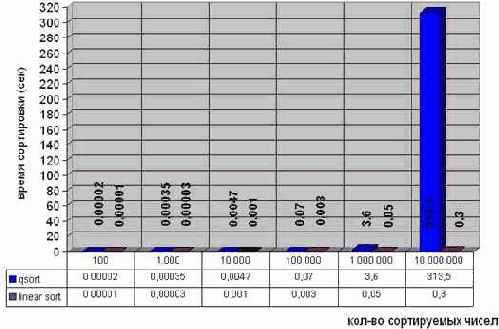
Рисунок 55 graph 0x33 Время сортировки различного количества чисел алгоритмами quick sort и linear sort
Ведь существует же весьма простой и эффективный алгоритм сортировки, требующий в худшем случае порядка O(n) операций. Нет, это не шутка и не первоапрельский розыгрыш! Такой алгоритм действительно есть.
Так, на компьютере AMD Athlon 1050 он упорядочивает десять миллионов чисел всего 0,3 сек, что в тысячу раз быстрее quick sort!
Впервые с этим алгоритмом мне пришлось столкнуться на олимпиаде по информатике, предлагающей в одной из задач отсортировать семь чисел, используя не более трех сравнений. Решив, что по такому поводу не грех малость повыпендриваться, я быстро написал программку, которая выполняла сортировку, не используя вообще ни одного сравнения. К сожалению, по непонятным для меня причинам, решение зачтено не было, и только спустя пару лет, изучив существующие алгоритмы сортировки, я смог оценить не тривиальность полученного результата.
Собственно, вся идея заключалась в том, что раз неравенство k + 1 > k > k – 1 справедливо для любых k, то можно сопоставить каждому числу kx соответствующую ему точку координатной прямой и в итоге мы получим… "естественным образом" отсортированную последовательность точек. Непонятно? Давайте разберем это на конкретном примере. Пусть у нас имеются числа 9, 6, 3 и 7. Берем первое из них – 9 – отступаем вправо на девять условных единиц от начала координатной прямой и делам в этом месте зарубку. Затем берем следующее число – 6– и повторяем с ним ту же самую операцию… В конечном счете у нас должно получится приблизительно следующее (см. рис. 44).
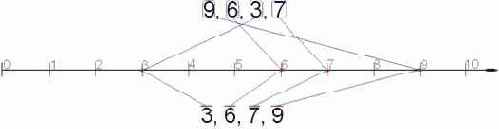
Рисунок 56 0х44 Сортировка методом отображения
А теперь давайте, двигаясь по координатной прямой слева направо просто выкинем все неотмеченные точки (или, иначе говоря, выделим отмеченные). У нас получится… получиться последовательность чисел, упорядоченная по возрастанию! Соответственно, если двигаться по прямой справа налево, мы упорядочим числа по убыванию.
И вот тут мы подходим к самому интересному! Независимо от расположения сортируемых чисел, количество операций, необходимых для их упорядочивания, всегда равно: N+VAL_N, где N – количество сортируемых чисел, а VAL_N – наибольшее количество значений, которые могут принимать эти числа.
Поскольку, VAL_N константа, из формулы оценки сложности алгоритма ее можно исключить и тогда она (формула сложности) будет выглядеть так: O(N). Wow! У вам уже чешутся руки создать свою первую реализую? Что ж, это нетрудно. Заменим числовую ось одномерным массивом и вперед:
#define DOT 1
#define NODOT 0
int a;
int src[N];
int coordinate_line[VAL_N];
memset(coordinate_line, NODOT, VAL_N*sizeof(int));
// ставим на прямой зарубки в нужных местах
for (a = 0; a < N; a++)
coordinate_line[src[a]]=DOT;
// просматриваем прямую справа налево в поисках зарубок
// все "зарубленные" точки копируем в исходный массив
for(a = 0; a < N_VAL; a++)
if (coordinate_line[a]) { *src = a; src++;}
Листинг 44 Простейший вариант реализации алгоритма линейной сортировки
Ага! Вы уже заметили один недостаток этой реализации алгоритма? Действительно, побочным эффектом такой сортировки становится отсечение всех "дублей", т.е. совпадающих чисел. Возьмем, например, такую последовательность: 3, 9, 6, 6, 3, 2, 9. После сортировки мы получим: 2, 3, 6, 9. Знаете, а с одной стороны это очень даже хорошо! Ведь зачастую "дубли" совершенно не нужны и только снижают своим хламом производительность.
Хорошо, а как быть если уничтожение дублей в таком-то конкретном случае окажется неприемлемо? Нет ничего проще, – достаточно лишь слегка модифицировать наш алгоритм, не просто ставя зарубку на координатной прямой, но еще и подсчитывая их количество в соответствующей ячейке массива. Усовершенствованный вариант реализации может выглядеть, например, так:
int* linear_sort(int *p, int n)
{
int N;
int a, b;
int count = 0;
int *coordinate_line; // массив для сортировки
// выделяем память
coordinate_line = malloc(VAL_MAX*sizeof(int));
if (!coordinate_line) /* недостаточно памяти */
return 0;
// init
memset(coordinate_line, 0, VAL_MAX*sizeof(int));
// сортировка
for(a = 0; a < n; a++)
coordinate_line[p[a]]++;
// формирование ответа
for(a = 0; a < VAL_MAX; a++)
for(b = 0; b < coordinate_line[a]; b++)
p[count++]=a;
// освобрждаем память
free(coordinate_line);
return p;
}
Листинг 45 [Memory/sort.linear.c] Пример улучшенной реализации алгоритма линейной сортировки
Давайте сравним его с quick sort при различных значениях N и посмотрим насколько он окажется эффективен. Эксперименты, проведенные автором, показали, что даже такая примитивная реализация линейной сортировки намного превосходит quick sort и при малом, и при большом количестве сортируемых значений (см. рис. graph 32). Причем, этот результат можно существенно улучшить если прибегнуть к услугам разряженных массивов, а не тупо сканировать virtual_array целиком!
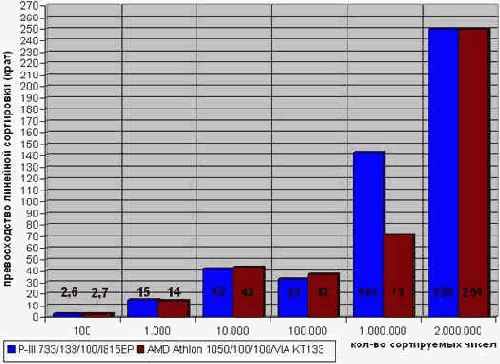
Рисунок 57 graph 32 Превосходство линейной сортировки над qsort. Смотрите, линейная сортировка двух миллионов чисел (вполне реальное количество, правда) выполняется в двести пятьдесят раз быстрее!
Но не все же время говорить о хорошем! Давайте поговорим и о печальном. Увы, за быстродействие в данном случае приходится платить оперативной памятью. Алгоритм линейной сортировки пожирает ее прямо-таки в чудовищных количествах. Вот приблизительные оценки.
Очевидно, количество ячеек массива coordinate_line
равно количеству значений, которые могут принимать сортируемые данные. Для восьми битных типов char это составляет 28=256 ячеек, для шестнадцати и тридцати двух битных int – 216= 65.536 и 232= 4.294.967.296 соответственно. С другой стороны, каждая ячейка массива coordinate_line
должна вмещать в себя максимально возможное количество дублей, что в худшем случае составляет N. Т.е. в большинстве ситуаций под нее следует отводить не менее 16, а лучше все 32 бита. Учитывая это, составляем следующую нехитрую табличку.
|
тип данных |
кол-во требуемой памяти при сохранении дублей |
кол-во требуемой памяти без сохранения дублей |
|
char |
1 Кб |
32 байта |
|
char (без учета знака) |
512 байт |
16 байт |
|
_int16 |
256 Кб |
8 Кб |
|
_int16 (без учета знака) |
128 Кб |
4 Кб |
|
_int32 |
16 Гб |
1 Гб |
|
_int32 (без учета знака) |
8 Гб |
256 Кб |
Таблица 5 Количество памяти, потребляемой алгоритмом линейной сортировки при упорядочивании данных различного типа
Ничегошеньки себе потребности! Для сортировки 32-разядных элементов с сохранением "дублей" потребуется восемь гигабайт оперативной памяти! Конечно, 99.999% ячеек памяти будут пустовать и потому подкачка страниц с диска не сильно ухудшит производительность, но… Вся проблема как раз и заключается в том, что нам просто не дадут этих восьми гигабайт. Операционные системы Windows 9x/NT ограничивают адресное пространство процессора всего четырьмя гигабайтами, причем больше двух из них расходуется на "служебные нужны" и максимально доступный объем кучи составляет гигабайт - полтора.
Правда, можно поровну распределить массив coordinate_line
между восемью процессами (ведь возможность читать и писать в "чужое" адресное пространство у нас есть – см. описания функций ReadProcessMemory и WriteProcessMemory в Platform SDK). Конечно, это очень кривое и уродливое решение, но зато крайне производительное. Ну пусть за счет накладных расходов на вызов API-функций алгоритм линейной сортировки превзойдет quick sort не в тысячу, а в шестьсот–девятьсот раз. Все равно он будет обрабатывать данные на несколько порядков быстрее.
Впрочем, ведь далеко не всегда сортируемые данные используют весь диапазон значений _int32: от –2,147,483,648 до 2,147,483,647. А раз так, – потребности в памяти можно существенно сократить! Действительно, количество требуемой памяти составляет: Cmem = N_VAL*sizeof(cell), где N_VAL – кол-во допустимых значений, а sizeof(cell) – размер ячеек, хранящих "зарубки" (они же – дубли). В частности, для сортировки данных диапазона [0; 1.000.000] потребуется не более 4 мегабайт памяти. Это весьма незначительная величина!
Сортировка вещественных типов данных.
До сих пор мы говорили лишь о сортировке целочисленных типов данных, между тем программистам приходится обрабатывать и строки, и числа с плавающей запятой, и...
Первоначально предложенный мной алгоритм действительно поддерживал работу лишь с целыми числами, но после публикации статьи "Немного о линейной сортировке" (ее и сейчас можно найти в сети…) им заинтересовались остальные программисты, среди которых были и те, кто приспособил линейную сортировку под свои нужды.
В частности, линейную сортировку вещественных чисел первым (насколько мне известно) реализовал Дмитрий Коробицын, письмо которого приводится ниже:
----- Original Message -----
From: "Дмитрий
Коробицын" <dvk@nts.ru>
To: "Крис Касперски" <kk@sendmail.ru>
Sent: Friday, June 22, 2001 2:27 AM
Subject: Re: О линейной сортировке
ДК> Сегодня хочу написать про сортировку чисел Float.
ДК> Вы пишете:
КК>> Один только ньюанс - как отсортировать числа по возрастанию? Формат
КК>> float и dooble не сложен, но попробуй-ка вывести все числа в порядке
КК>> возрастания!
Да, действительно для сортировки чисел Float придется построить функцию long int f(float x), такую, чтобы для любых x и y, если x<y, то f(x) < f(y). Не вызывает сомнения, что такую функцию построить можно, но весь вопрос в том, насколько она сложна и сколько шагов потребуется от компьютера для ее реализации? Сразу оговоримся, что трудоемкость этой функции от размера массива чисел не зависит, следовательно это константа, и на трудоемкость всего алгоритма она повлиять не сможет. Он так и останется линейным. Чтобы сильно не злоупотреблять Вашим вниманием, забегая вперед, хочу сразу сказать, что эта функция очень простая. Проще не бывает. Это "функция правды", как Вы назвали ее в одной из своих статей, а именно f(x) = x, то есть преобразовывать ничего не нужно. Нужно просто компилятору сказать, что в этих ячейках лежит не число float, a long int.
Доказательство: Float устроен следующим образом: 32 бита в памяти, самый старший бит это знак, тоже и у четырехбайтового целого числа. После бита знака следующие 8 битов "смещенный порядок" - показатель степени двойки.
Для положительных чисел float, чем больше порядок, тем больше число, но, с другой стороны, для положительного длинного целого чем большее число записано в старших битах, тем число больше. Оставшиеся 23 разряда – это значащая часть числа, мантисса. Значение положительного числа float получается следующим образом:
Значение = (1+мантисса*2^(-23)) * 2 ^ (смещенный порядок -127) Здесь следует пояснить, что если мантисса равна нулю, то значение числа float совпадает со степенью двойки. Если все биты мантиссы установлены в 1 (самая большая мантисса = 0x7FFFFF = 2^23 - 1), то получаем 1 + 0x7FFFFF*2^(-23) = 1.99999988079071044921875
Получаем, что для положительных float при одинаковом значении "смещенного порядка" чем больше мантисса, тем больше число, но для длинного целого та же ситуация, при одинаковых старших битах чем большее значение записано в младших битах тем больше число. Рассмотрим еще ситуацию, когда при увеличении числа меняется "смещенный порядок".
Возьмем для примера числа 1.99999988079071044921875 и 2.0 оба этих числа положительные, значит старший бит равен нулю. У первого показатель степени двойки равен 0 значит "смещенный порядок" = 127 = 0111 1111. Мантисса состоит вся из 1.
Следовательно в памяти это будет выглядеть так - старшие два бита равны 0, остальные - 1. У второго числа показатель степени двойки равен 1, а значение мантиссы равно 0. Смещенный порядок = 128 = 1000 0000. В памяти - все биты кроме второго равны 0.
Шестнадцат. Целое число Float
0x3F FF FF FF 1073741823 1.99999988079071044921875
0x40 00 00 00 1073741824 2.0
Еще несколько чисел:
Шестнадцат. Целое число Float
0x3D CC CC CD 1036831949 0.100000001490116119
0x3E 4C CC CD 1045220557 0.200000002980232239
0x3E 99 99 9A 1050253722 0.300000011920928955
0x3E CC CC CD 1053609165 0.400000005960464478
0x3F 00 00 00 1056964608 0.5
0x3F 19 99 9A 1058642330 0.60000002384185791
0x3F 33 33 33 1060320051 0.699999988079071045
0x3F 4C CC CD 1061997773 0.800000011920928955
0x3F 66 66 66 1063675494 0.89999997615814209
0x3F 80 00 00 1065353216 1.0
0x40 00 00 00 1073741824 2.0
0x40 40 00 00 1077936128 3.0
0x40 80 00 00 1082130432 4.0
0x40 A0 00 00 1084227584 5.0
0x40 C0 00 00 1086324736 6.0
0x40 E0 00 00 1088421888 7.0
0x41 00 00 00 1090519040 8.0
0x41 10 00 00 1091567616 9.0
0x41 20 00 00 1092616192 10.0
Из приведенной таблицы видно, что при возрастании числа float возрастает и соответствующее ему целое число. Заметим, что целое число ноль соответствует нулю с плавающей точкой.
Таким образом, для неотрицательных чисел никакого преобразования не требуется. Как же быть с отрицательными числами?
Отрицательные целые числа хранятся в дополнительном формате,то есть целому числу минус один соответствует 0xFF FF FF FF, а это самое большое по модулю отрицательное число (в действительности компьютер считает, что это "нечисло"). Числу минус десять миллионов соответствует float примерно равный минус три на десять в 38 степени.
Шестнадцат. Целое число Float
0xFF 67 69 80 -10000000 -3.07599454344890991e38
0xFA 0A 1F 00 -100000000 -1.79291430293879854e35
0xC4 65 36 00 -1000000000 -916.84375
0xC0 00 00 00 -1073741824 -2.0
0xBF 80 00 00 -1082130432 -1.0
0xBF 00 00 00 -1090519040 -0.5
0xA6 97 D1 00 -1500000000 -1.05343793584122825e-15
0x88 CA 6C 00 -2000000000 -1.21828234519221877e-33
Из приведенной таблицы видно, что чем больше по модулю отрицательное целое число, тем меньше по модулю число float. Неужели придется проверять знак у числа, и если оно отрицательное, то делать преобразование? На самом деле нехитрым программистским приемом избавляемся от всяких преобразований. Сначала прейдем от целых чисел со знаком к целым числам без знака. При этом преобразования не потребуются, просто область памяти вместо long int надо определить как unsigned long. (Заметим, что на сортировку положительных чисел это никак не повлияет.) Далее заметим, что самому большому по модулю отрицательному числу float вместо минус единицы теперь будет соответствовать 0xFF FF FF FF – это (два в степени 32) - 1.
Таким образом, самое большое целое число без знака будет соответствовать самому большому по модулю отрицательному числу. Но если теперь у нас все целые числа не имеют знака, то как же отделить положительные float от отрицательных? Потребуются преобразования? Нет!
Пример программы:
Программу напишем в виде функции, которой на вход передается не отсортированный массив float и его размер - n. После работы функции массив должен быть отсортирован по возрастанию.
void Sort(float *u, unsigned long N)
{
unsigned long *a,*int_u, c, n, k;
PrepareMem(&a);
// преобразуем указатель. Предполагая, что
sizeof(float) = sizeof(long)
int_u=(unsigned long *)u;
// сортировка
for (c=0; c < N; c++) a[int_u[c]]++;
// формируем отсортированный массив
k=0;
// сначала отрицательные числа, начиная с самых больших по модулю
for(c=0xFFFFFFFF; c > 0x7FFFFFFF; c--)
for(n=0; n < a[c]; n++)int_u[k++]=с;
// теперь положительные числа, начиная с (float) нуля.
for(c=0; c < 0x80000000; c++)
for(n=0; n < a[c]; n++)int_u[k++]=с;
}
Заметим, что инициализация памяти выделена в отдельную функцию. Во-первых, не плохо было бы проверить, чем закончилось выделение 16 гигабайт памяти. Во-вторых, на забивание массива нулями тратится почти половина времени работы алгоритма. Я предполагаю, что используя прямой доступ к памяти (DMA) это время можно сократить.
---- конец письма ---
Оптимизация ссылочных структур данных
Итак, если мы не хотим, чтобы наша программа ползала со скоростью черепахи в летний полдень и на полную использовала преимущества высокопроизводительной DDR- и DRRAM памяти, – следует обязательно устранить зависимость по данным. Как это сделать?
Вот скажем, графический файл в формате BMP, действительно, можно обрабатывать и параллельно, поскольку он представляет собой однородный массив данных фиксированного размера. Совсем иная ситуация складывается с двоичными деревьями, списками и прочими ссылочными структурами, хранящими разнородные данные.
Расщепление списков (деревьев). Рассмотрим список, "связывающий" пару десятков мегабайт текстовых строк переменной длины. Как оптимизировать прохождение по списку, если адрес следующего элемента заранее неизвестен, а список к тому же сильно фрагментирован? Первое, что приходит на ум: разбить один список на несколько независимых списков, обработка которых осуществляется параллельно. Остается выяснить: какая именно стратегия разбиения наиболее оптимальна. В этом нам поможет следующая тестовая программа, последовательно прогоняющая списки с различной степенью дробления (1:1, 1:2, 1:4, 1:6 и 1:8). Ниже, по соображениям экономии бумажного пространства, приведен лишь фрагмент, реализующий комбинации 1:1 и 1:2. Остальные же степени дробления реализуются полностью аналогично.
#define BLOCK_SIZE (12*M) // размер обрабатываемого блока
struct MYLIST{ // элемент списка
struct MYLIST *next;
int val;
};
#define N_ELEM (BLOCK_SIZE/sizeof(struct MYLIST))
/* -----------------------------------------------------------------------
*
* обработка одного списка
*
----------------------------------------------------------------------- */
// инициализация
for (a = 0; a < N_ELEM; a++)
{
one_list[a].next = one_list + a + 1;
one_list[a].val = a;
} one_list[N_ELEM-1].next = 0;
// трассировка
p = one_list;
while(p = p[0].next);
/* -----------------------------------------------------------------------
*
* обработка двух расщепленных списков
*
----------------------------------------------------------------------- */
// инициализация
for (a = 0; a < N_ELEM/2; a++)
{
spl_list_1[a].next = spl_list_1 + a + 1;
spl_list_1[a].val = a;
spl_list_2[a].next = spl_list_2 + a + 1;
spl_list_2[a].val = a;
} spl_list_1[N_ELEM/2-1].next = 0;
spl_list_2[N_ELEM/2-1].next = 0;
// трассировка
p1 = spl_list_1; p2 = spl_list_2;
while((p1 = p1[0].next) && (p2 = p2[0].next));
// внимание! Данный способ трассировки предполагает, что оба списки
// равны по количеству элементов, в противном случае потребуется
// слегка доработать код, например, так:
// while(p1 || p2)
// {
// if (p1) p1 = p1[0].next;
// if (p2) p2 = p2[0].next;
// }
// однако это сделает его менее наглядным, поэтому в книге приводится
// первый вариант
Листинг 11 [Memory/list.splint.c] Фрагмент программы, определяющий оптимальную стратегию расщепления списков
На P-III 733/133/100/I815EP заметна ярко выраженная тенденция уменьшения времени прохождения списков, по мере приближения степени дробления к четырем. При этом быстродействие программы возрастает более чем в полтора раза (точнее – в 1,6 раз)! Дальнейшее увеличение степени дробления лишь ухудшает результат (правда незначительно). Причина в том, что при параллельной обработке более чем четырех потоков данных происходят постоянные открытия/закрытия DRAM-страниц, "съедающие" тем самым весь выигрыш от параллелизма (подробнее см. "Планирование потоков данных").
На AMD Athlon 1050/100/100/VIA KT133 ситуация совсем иная. Поскольку, и сам процессор Athlon, и чипсет VIA KT133 в первую очередь оптимизирован для работы с одним потоком данных, параллельная обработка расщепленных списков ощутимо снижает производительность.
Впрочем, расщепление одного списка на два все-таки дает незначительный выигрыш в производительности. Однако, наиболее оптимальна стратегия расщепления отнюдь не на два, и даже не на четыре, а… на шесть списков. Именно шесть списков обеспечивают наилучший компромисс при оптимизации программы сразу под несколько процессоров.
Разумеется, описанный прием не ограничивается одними списками. Ничуть не менее эффективно расщепление двоичных деревьев и других структур данных, в том числе и не ссылочных.
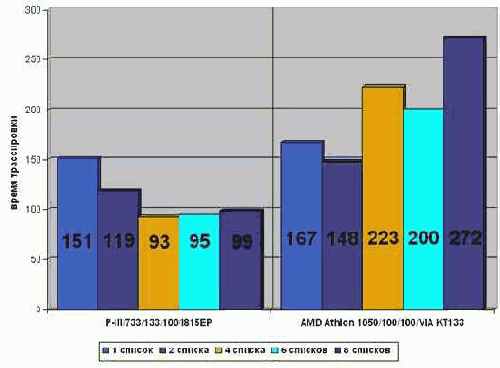
Листинг 12 graph 20 Зависимость времени обработки данных от степени расщепления списков. Как видно, наилучшая стратегия заключается в шестикратном расщеплении списков. Это обеспечивает наилучший компромисс для обоих процессоров
Быстрое добавление элементов. Чтобы при добавлении нового элемента в конец списка не трассировать весь список целиком, сохраняйте в специальном после ссылку на последний элемент списка. Это многократно увеличит производительность программы, под час больше чем на один порядок (а то и на два-три).
Подробнее об этом см. "Оптимизация строковых штатных Си-функций". Какое отношение имеют строки к спискам? Да самое непосредственное! Ведь строка это одна из разновидностей вырожденного списка, не сохраняющего ссылку на следующий элемент, а принудительно располагающая их в памяти так, чтобы они строго следовали один за другим.
Оптимизация строковых штатных Си-функций
С разительным отличием скорости обработки двойных слов и байтов мы уже столкнулись (см. "Обработка памяти байтами, двойными и четвертными словами"). Теперь самое время применить наши знания для оптимизации строковых функций.
Типичная Си-строка (см. рис. 41) представляет собой цепочку однобайтовых символов, завершаемую специальным символом конца строки – нулевым байтом (не путать с символом "0"!), поэтому Си-строки так же называют ASCIIZ-стоками ('Z' – сокращение от "Zero", – нуль на конце). Это крайне неоптимальная структура данных, особенно для современных 32?разрядных процессоров!
Основной недостаток Си-строк заключается в невозможности быстро определить их длину, – для этого нам приходится сканировать всю строку целиком в поисках завершающего ее нуля. Причем, поиск завершающего символа должен осуществляется побайтовым сравнением каждого символа строки с нулем. А ведь производительность побайтового чтения памяти крайне низка! Конечно, можно попробовать сделать "ход котом": загружать ячейки памяти двойными словами, а затем "просвечивать" их сквозь четыре битовых маски, только вряд ли это добавит производительности, – скорее лишь сильнее ухудшит ее.
По тем же самым причинам невозможно реализовать эффективное копирование и объединение Си-строк. Действительно, как прикажете копировать строку не зная какой она длины?
В довершении ко всему, Си-строки не могут содержать символа нуля (т.к. он будет ошибочно воспринят как завершитель строки) и потому плохо подходят для обработки двоичных данных.
Всех этих недостатков лишены Pascal-строки, явно хранящие свою длину в специальном поле, расположенном в самом начале строки. Для вычисления длины Pascal-строки достаточно всего одного обращения к памяти (грубо говоря, длина Pascal-строк может быть вычислена мгновенно). /* Кстати, при работе с любыми структурами данных, в частности, со списками, настоятельно рекомендуется сохранять в специальном после ссылку на последний элемент, чтобы при добавлении новых элементов в конец списка не приходилось каждый раз трассировать его целиком */
Как это обстоятельство может быть использовано для оптимизации копирования и объединения Pascal-строк? А вот смотрите:
char *с_strcpy(char *dst, char *src) char *pascal_strcpy(char *dst, char *src)
{ {
char * cp = dst; int a;
while( *cp++ = *src++ ); for(a=0; a < ((*src+1) & ~3); a += 4)
// копируем строку по байтам *(int *)(dst+a)=*(int *)(src+a);
// одновременно с этим проверяя // копируем строку двойными словами
// каждый символ на равенство нулю // проверять каждый символ на равенство
// нулю в данном случае нет необходимости
// т.к. длина строки наперед известна
for(a=((*src+1) & ~3); a<(*src+1); a ++)
*(char *)(dst+a)=*(char *)(src+a);
// копируем остаток хвоста строки
// (если он есть) по байтам.
// это не снижает производительности,
// т.к. максимально возможная длина
// хвоста составляет всего три байта
return( dst ); return( dst );
} }
Листинг 39 Пример реализации функций копирования Си (слева) и Pascal строк (справа)
char *с_strcat (char *dst, char *src) char *pascal_strcat (char *dst, char *src)
{ {
char *cp = dst; int len;
while( *cp ) ++cp; len=*dst;
// читаем всю строку-источник // за одно обращение к памяти
// байт за байтом в поисках // определяем длину строки-приемника
// ее конца
*dst+=*src;
// корректируем длину строки-приемника
while( *cp++ = *src++ ); pascal_strcpy(dst+len,src);
// байт за байтом дописываем // копируем строку двойными словами
// источник к концу приемника,
// до тех пор пока не встретим нуль
return( dst ); return( dst );
} }
Листинг 40 Пример реализации функций объединения Си (слева) и Pascal строк (справа)
Итак, в отличие от Си-строк, Pascal-строки допускают эффективную блочную обработку и при желании могут копироваться хоть восьмерными словами. Другое немаловажное обстоятельство: при объединении Pascal-строк нам незачем просматривать всю строку-приемник целиком в поисках ее конца, поскольку конец строки определяется алгебраическим сложением указателя на начала строки с первым байтом строки, содержащим ее длину.
Интенсивная работа с Си-строками способна серьезно подорвать производительность программы и потому лучше совсем отказаться от их использования. Проблема в том, что мы не можем "самовольно" перейти на Pascal-строки, не изменив все сопутствующие им библиотеки языка Си и API-функций операционной системы. Ведь функции наподобие fopen или LoadLibrary рассчитаны исключительно на ASCIIZ-строки и попытка "скормить" им Pascal?строку ни к чему хорошему не приведет, – функция, не обнаружив в положенном месте символа-завершителя строки, залезет совершенно в постороннею память!
Выход состоит в создании "гибридных" Pascal + ASCIIZ-строк, явно хранящих длину строки в специально на то отведенном поле, но вместе с тем, имеющих завершающий ноль на конце строки. Именно так и поступили разработчики класса CString библиотеки MFC, распространяемой вместе с компилятором Microsoft Visual C++.

Рисунок 51 0х41 Устройство Си, Pascal, Delphi и MFC-строк.
Си- строки могут иметь неограниченную длину, но не могут содержать в себе символа нуля, т.к. он трактуется как завершитель строки. Pascal-строки хранят длину строки в специальном однобайтовом поле, что значительно увеличивает эффективность строковых функций, позволяет хранить в строках любые символы, но ограничивает их размер 256 байтами. Delphi-строки представляют собой разновидность Pascal-строк и отличаются от них лишь увеличенной разрядностью поля длины, теперь строки могут достигать 64Кб длины. MFC-строки – это гибрид Си и Pascal строк с 32-битным полем длины, благодаря чему макс. длина строки теперь равна 4Гб.
Несложный тест (см. [Memory/MFC.c]) поможет нам сравнить эффективность обработки Си- и MFC-строк на операциях сравнения, копирования и вычисления длины. На последней операции, собственно, и наблюдается наибольших разрыв в производительности, достигающих в зависимости от длины "подопытной" строки от одного до нескольких порядков.
Объединение двух MFC-строк (при условии, что обе они одинаковой длины) осуществляется практически вдвое быстрее, чем аналогичных им Си-строк, что совсем неудивительно, т.к. в первом случае мы обращаемся к вдвое меньшему количеству ячеек памяти. Разумеется, если к концу очень длиной строки дописывается всего несколько символов, то выигрыш от использования MFC-строк окажется много большим и приблизительно составит: крат.
А вот сравнение Си- и MFC- строк происходит одинаково эффективно, точнее одинаково неэффективно, поскольку разработчики библиотеки MFC- предпочли побайтовое сравнение сравнению двойными словами, что не самым лучшим образом сказалось на производительности. Забавно, но штатная функция strcmp из комплекта поставки Microsoft Visual C++ (не intrinsic!), – похоже единственная функция сравнения строк, обрабатывающая их не байтами, а двойными словами, что в среднем происходит вдвое быстрее. В общем, наиболее предпочтительное сравнение MFC-строк выглядит так:
#include <String.h>
#pragma function(strcmp) // вырубаем intrinsic'ы
if (strcmp(s0.GetBuffer(0),s1.GetBuffer(0)))
// строки не равны
else
// строки равны
Листинг 41 Пример эффективного сравнения MFC-строк
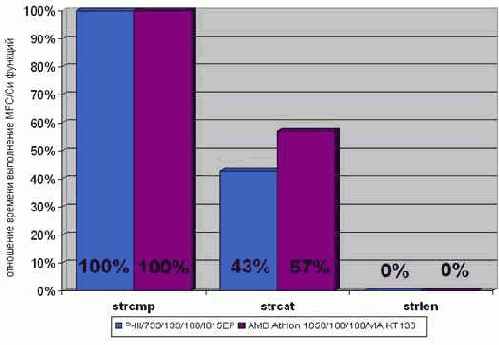
Рисунок 52 graph 24 Сравнение эффективности MFC и Си функций, работающий со строками. Как видно, MFC строки более производительны
Оптимизация структур данных под аппаратную предвыборку
Грамотное использование программной предвыборки позволят полностью забыть о существовании аппаратной и не брать особенностей последней в расчет. Это тем более предпочтительно, что механизмом аппаратной предвыборки на момент написания этой книги оснащен один лишь P-4 (прим. сейчас аппаратная предвыборка появилась и в старших моделях процессора AMDAthlon), да и перспектива его развития в последующих моделях весьма туманна. Однако, как уже было показано выше, в ряде случаев достижение эффективной работы программной предвыборки без индивидуальной "заточки" критического кода под конкретный процессор просто невозможно! Фактически это обозначает, что один и тот же фрагмент программы приходится реализовывать в нескольких ипостасях – отдельно под K6 (VIA C3), Athlon, P-II, P-III и P-4. Если все равно приходится оптимизировать программу под каждый процессор по отдельности, то почему бы задействовать возможности P-4 на всю мощь?
Поскольку, накладные расходы на программную предвыборку не равны нулю, следует отказаться от нее везде, где и аппаратная предвыборка справляется хорошо. В первую очередь это – многократно повторяемые циклы, обрабатывающие данные по регулярным шаблонам. Причем на страницу должно приходиться не более одного потока, а общее количество потоков – не превышать восьми. Например, так:
int x[BIGNUM];
for(a=0;a<BIGNUM, a++)
sum+= x[a];
Листинг 30 Пример кода, эффективно оптимизируемый аппаратной предвыборкой – один регулярный шаблон на страницу
А вот незначительная модификация предыдущего примера – теперь в цикле суммируется не один массив, а сразу два:
int x[256];
int y[256];
for(a=0;a<256, a++)
{
sum1+= x[a];
sum2+= y[a];
}
Листинг 31 Пример кода, "ослепляющий" аппаратную предвыборку – два шаблона на страницу
Поскольку, оба массива расположены в пределах одной страницы, механизм аппаратной предвыборки "слепнет" и упреждающая загрузка данных не осуществляется. Повысить эффективность выполнения кода можно либо разбив один цикл на два, каждый из которых будет обрабатывать "свой" массив, либо разнести массивы x
и y
так, чтобы их разделяло более четырех килобайт (внимание: этого нельзя достичь, просто поместив между ними еще один массив, т.к. порядок размещения массивов в памяти целиком лежит на "совести" компилятора и не всегда совпадает с порядком их объявления в программе), либо… преобразовать два массива в массив элементов одной структуры:
struct ZZZ{int x; int x;} zzz[1024];
for(a=0;a<1024, a++)
{
sum1+= zzz.x[a];
sum2+= zzz.y[a];
}
Листинг 32 Исправленный пример листинга ???12 – один регулярный шаблон на страницу
На первый взгляд непонятно, что дает такое преобразование – ведь по-прежнему, на одну страницу приходится два регулярных шаблона. Да, это так – но в последнем случае оба шаблона сливаются в один общий шаблон. Если до этого происходило обращение к N, N+1024, N+4, N+1028, N+8, N+1032 ячейками памяти, то теперь: N, N+4, N+8, N+12… вот и весь фокус!
Кстати, всегда следует помнить, что шаблон определяется не адресами ячеек, к которым происходит обращение, а адресами ячеек, которые вызывают кэш-промах. Совсем не одно и то же! Благодаря этому обстоятельству в пределах всякого 128-байтового блока памяти, уже находящегося в L2-кэше, можно обращаться и по нерегулярному шаблону – лишь бы сами 128-байтовые блоки запрашивались регулярно.
Но вернемся к нашим баранам. Как вы думаете, сможет ли эффективно выполняться на P-4 следующий пример?
struct ZZZ{int x; int x; int sum; } zzz[BIGNUM];
for(a=0;a<BIGNUM, a++)
{
zzz.sum[a]=zzz.x[a]+zzz.y[a];
}
Листинг 33 Пример кода, "ослепляющего" аппаратную предвыборку – и чтение, и запись в пределах одной страницы
Конечно же, он будет исполняться неэффективно! Поскольку в пределах одной страницы осуществляется и чтение, и запись, аппаратная предвыборка не осуществляется. Как быть? Если массив zzz содержит не менее 1024 элементов, разбив структуру ZZZ на три независимых массива, мы добьемся того, что чтение и запись будут происходить в различные страницы:
int x[BIGNUM]; int x[BIGNUM]; int sum[BIGNUM];
for(a=0;a<BIGNUM, a++)
{
sum[a]=x[a]+y[a];
}
Листинг 34 Исправленный вариант листинга ??? 14 – чтение и запись происходят в различные страницы
Кстати, будет не лишним отметить, что такой прием существенно замедляет эффективность выполнения кода на всех остальных процессорах. Почему? Вспомним, что размещение данных в пределах одной DRAM-страницы значительно уменьшает ее латентность, т.к. для доступа к ячейке достаточно передать лишь номер ее столбца, а номер строки будет тот же самый, что и в прошлый раз.
Поочередное обращение к данным, расположенным в различных DRAM-страницах, напротив, требует передачи полного адреса ячейки, а это как минимум 2-3 такта системной шины. Но, если на P-4 латентность компенсируется аппаратной предвыборкой данных, на других процессорах ее скомпенсировать нечем! Вот еще одно подтверждение того, что код, оптимальный для P-4 не всегда оптимален для остальных процессоров, и, соответственно, наоборот…
_загрузка кода,
Оптимизация заполнения (инициализации) памяти
Техника оптимизации копирования памяти в целом применима и к ее инициализации – заполнению блока памяти некоторым значением (чаще всего нулями). Эта операция обычно осуществляется либо стандартной функцией языка Си memset, либо win32 функцией FillMemory. (Впрочем, на самом деле это одна и та же функция – в заголовочном файле WINNT.h макрос FillMemory определен как RtlFillMemory, а RtlFillMemory на x86 платформе определен как memset).
Подавляющее большинство реализаций функции memset использует инструкцию циклической записи в память REP STOSD, инициализирующей одно двойное слово за одну итерацию. Но, в отличие от REP MOVSD, она требует совсем другого выравнивания. Причем, об этом обстоятельстве не упоминает ни Intel, ни AMD, ни сторонние руководства по оптимизации!
Достаточно неожиданным эффектом инициализации ячеек памяти уже находящихся в кэше первого (а на P-III+ и второго) уровня является существенное увеличение производительности при выравнивании начального адреса по границе 8 байт. На P-II и P-III в этом случае за 32 такта выполняется 42 итерации записи двойных слов. Рекомендуемое же документацией выравнивание по границе 4 байт дает гораздо худший результат – за 32 такта выполняется всего лишь 12 итераций, т.е. в три с половиной раза меньше!
Это объясняется тем, что в первом случае не тратится время на выравнивание внутренних буферов и строк кэша – сброс данных происходит по мере заполнения буфера и не интерферирует с операциями выравнивания. Поскольку разрядность шины (и буфера) - 64 бита (8 байт), выбор начального адреса, не кратного 8, приводит к образованию "дыры" в 4 байта и, прежде чем свалить данные, потребуется выровнять буфер к кэшу и "закрасить" недостающие 4 байта. А это – время.
Сказанное справедливо не только для инструкции REP STOS, но и вообще для любой циклической записи – не важно слов, двойных слов или даже байт. Поэтому, многократно инициализируемые структуры данных, на момент инициализации уже находящиеся в кэше, целесообразно выравнивать по адресам, кратным восьми.
Циклическая запись в область памяти, отсутствующую в кэше – совсем другое дело. Выравнивание начального адреса по границе восьми байт, ничем не предпочтительнее четырех. Причем, на P-III начальный адрес можно вообще не выравнивать, т.к. выигрыш измеряется долями процента. Правда, на P-II цикл записи, начинающийся с адреса не кратного четырем, замедляется более чем в два раза. Такой существенный проигрыш никак нельзя не брать в расчет, даже в свете того, что парк P-II с каждым годом будет все сильнее и сильнее истощаться.
Сказанное наглядно иллюстрируют графики, приведенные на рис. 0x27 и рис. 0x028, изображающие зависимость скорости инициализации блоков памяти различного размера от кратности начального адреса на процессорах Pentium-II и Pentium-III. (см. программу memstore_align).
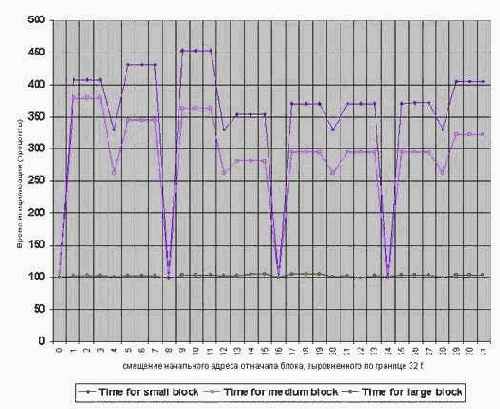
Рисунок 52 graph 0x027 График зависимости времени инициализации блоков памяти различного размера от кратности начального адреса. [Pentium-III 733/133/100]
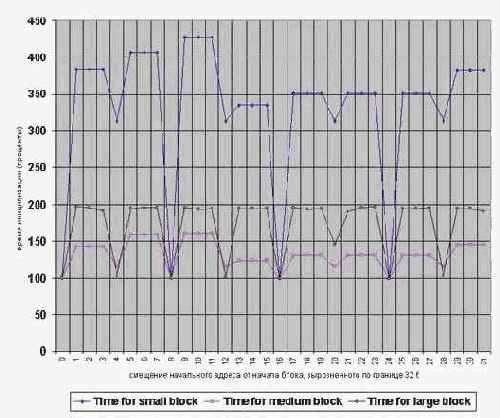
Рисунок 53 graph 0x028 График зависимости времени инициализации блоков памяти различного размера от кратности начального адреса. [CELERON-300A/66/66]
Скорость записи ячеек памяти, отсутствующих в кэше крайне непостоянна и зависит в первую очередь от состояния внутренних буферов процессора. Время инициализации небольших, порядка 4-8 килобайт блоков, может отличаться в два и более раз, особенно если операции записи следуют друг за другом всплошную – без пауз на сброс буферов. Отсутствие пауз при инициализации большого количества блоков памяти приводит к образованию "затора" – переполнению кэша второго уровня и, как следствие, значительным тормозам. И хотя средне взятый разброс скорости записи при этом существенно уменьшается (составляя порядка 5%), на графике появляются высокие пики и глубокие провалы, причем пики традиционно предшествуют провалам. Их происхождение связано с переключением задач многозадачной операционной системой, - если остальные задачи не слишком плотно налегают на шину (что чаще всего и случается) буфера (или хотя бы часть из них) успевают выгрузиться и подготовить себя к эффективному приему следующей порции записываемых данных (см.
рис.???7).
Непостоянство скорости записи создает проблемы профилирования приложений – разные участки программы поставлены в разные условия. Тормоза одного участка вполне могут объясняться тем, что предшествующий ему код до отказа заполнил все буфера и теперь инициализация происходит крайне неэффективно – т.е. выражаясь словами одного сказочного героя "когда болит горло – лечи хвост".
Серьезные проблемы наблюдаются и при оптимизации функции инициализации памяти – большой разброс замеров скорости выполнения затрудняет оценку эффективности оптимизации. Приходится делать множество прогонов для вычисления "средневзвешенного" времени выполнения.
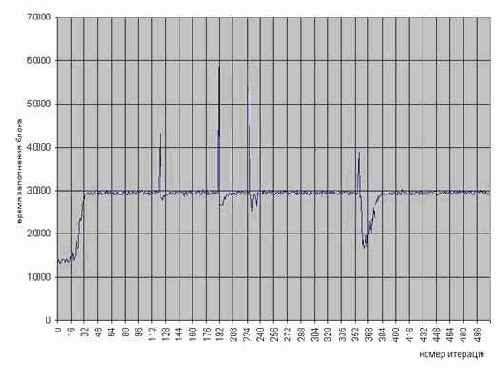
Рисунок 54 graph 0x023 График иллюстрирует непостоянность скорости записи ячеек памяти, отсутствующих в кэше (Бардовая линия). В данном примере последовательно обрабатывается 512 четырех килобайтных блока памяти. Для сравнения приведен график скорости копирования блоков памяти такого же точно размера (Синяя линия). Видно, что разброс скорости записи уменьшается при заполнении кэша второго уровня, в то время как разброс скорости копирования памяти остается постоянным. [Premium-III 733/133/100] (см. mem_mistake)
В отличие от копирования, инициализировать память всегда лучше в прямом направлении, независимо от того, как обрабатывается проинициализированный блок – с начала или с конца. Объясняется это тем, что запись ячейки, отсутствующей в кэше, не приводит к загрузке этой ячейки в кэш первого уровня – данные попадают в буфера, откуда выгружаются в кэш второго уровня. Поэтому, на блоках, не превышающих размера кэша второго уровня, никакого выигрыша заведомо не получится. Блоки, в несколько раз превосходящие L2-кэш, действительно, быстрее обрабатываются будучи проинициализированными с заду наперед, но выигрыш этот столь несущественен, что о нем не стоит и говорить. Обычно он составляет 5%-10% и "тонет" на фоне непостоянства скорости инициализации. (см. рис.???8)
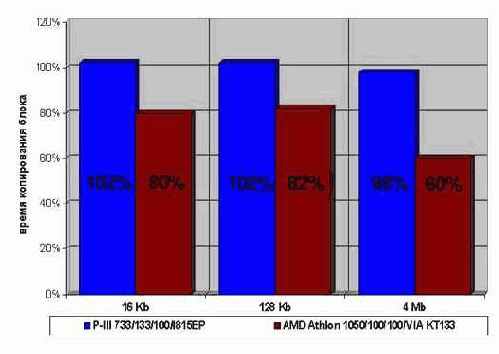
Рисунок 55 graph 0x024 Диаграмма иллюстрирует относительное время инициализации блоков памяти различного размера с последующей обработкой.
За 100% взято время инициализации штатной функции memset (синие столбики). и прямая инициализация небольшими блоками, обрабатываемыми от конца к началу (желтые столбики). [Pentium-III 733/133/100] (см. memstore_direct)
Оптимизация инициализации памяти в старших моделях процессоров Pentium. Инструкция некэшируемое записи восьмерных слов movntps, уже рассмотренная ранее, практически втрое ускоряет инициализацию памяти, при этом не "загаживая" кэш второго уровня. Это идеально подходит для инициализации больших массивов данных, которые все равно не помещаются в кэше, а вот инициализация компактных структур данных с их последующей обработкой – дело другое. На компактных блоках movntps заметно отстает от штатной функции memset, проигрывай ей в полтора-два раза, а на блоках умеренного размера, movntps хотя и лидирует, но обгоняет memset всего на 25%-30%, что ставит под сомнение целесообразность ее применения (ведь на P-II и более ранних процессорах ее нет!). (см. рис.???9)
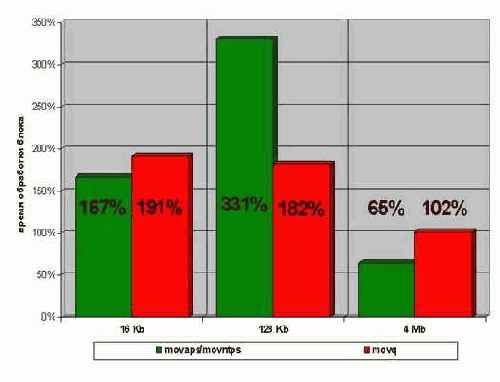
Рисунок 56 graph 0x025 Диаграмма иллюстрирует относительное время инициализации блоков памяти различного размера. За 100% взято время инициализации штатной функции memset (синие столбики). С нею состязаются инструкция копирования четверных слов movq (красные столбики) и инструкция не кэширующей записи восьмерных слов movntps (желтые и голубые столбики). Голубые столбики выражают скорость инициализации с последующей обработкой инициализированного блока.
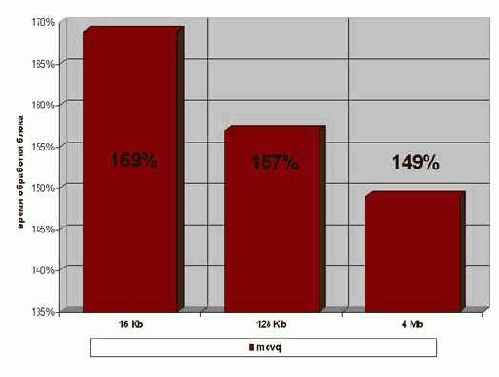
Рисунок 57 graph 0x026 Использование movq на AMD Athlon
адресация кэша - полинейная, адресация байтов в линии при помощи битов-атрибутов. любая райт-бэк операция эффективно транслируется в рид-модифай-райт.
Организация кэша
Для упрощения взаимодействия с оперативной памятью (и еще по ряду других причин), кэш-контроллер оперирует не байтам, а блоками данных, соответствующих размеру пакетного цикла чтения/записи (см. "ЧастьI. Оперативная память. Устройство и принципы функционирования оперативной памяти. Взаимодействие памяти и процессора."). Программно, кэш-память представляет собой совокупность блоков данных фиксированного размера, называемых кэш-линейками (cache-line) или кэш-строками.
Каждая кэш-строка полностью заполняется (выгружается) за один пакетный цикл чтения и всегда заполняется (выгружается) целиком. Даже если процессор обращается к одному байту памяти, кэш-контроллер инициирует полный цикл обращения к основной памяти и запрашивает весь блок целиком. Причем, адрес первого байта кэш-линейки всегда кратен размеру пакетного цикла обмена. Другими словам: начало кэш-линейки всегда совпадает с началом пакетного цикла.
Поскольку, объем кэша много меньше объема основной оперативной памяти, каждой кэш-линейке соответствует множество ячеек кэшируемой памяти, а отсюда с неизбежностью следует, что приходится сохранять не только содержимое кэшируемой ячейки, но и ее адрес. Для этой цели каждая кэш-линейка имеет специальное поле, называемое тегом. В теге хранится линейный и/или физический адрес первого байта кэш-линейки. Т.е. кэш-память фактически является ассоциативной памятью (associative memory) по своей природе.
В некоторых процессорах (например, в младших моделях процессоров Pentium) используется только один набор тегов, хранящих физические адреса. Это удешевляет процессор, но для преобразования физического адреса в линейный требуется по меньшей мере один дополнительный такт, что снижает производительность.
Другие же процессоры (например, AMD K5) имеют два набора тегов, для хранения физических и линейных адресов соответственно. К физическим тегам процессор обращается лишь в двух ситуациях: при возникновении кэш-промахов (в силу используемой в x86 процессорах схемы адресации одна и та же ячейка может иметь множество линейных адресов и потому несовпадение линейных адресов еще не свидетельство промаха) и при поступлении запроса от внешних устройств (в т.ч.
и других процессоров в многопроцессорных системах): имеется ли такая ячейка в кэш памяти или нет (см. "Протокол MESI"). Во всех остальных случаях используются исключительно линейные теги, что предотвращает необходимость постоянного преобразования адресов.
Доступ к ассоциативной памяти, в отличии от привычной нам адресной памяти, осуществляется не по номеру ячейки, а по ее содержанию, поэтому такой тип памяти еще называют content addressed memory. Кэш-строки, в отличии от ячеек оперативной памяти, не имеют адресов и могут нумероваться в произвольном порядке, да и то чисто условно. Выражение "кэш-контроллер обратился к кэш-линейке №69" лишено смысла и правильнее сказать: "кэш-контроллер, обратился к кэш-линейке 999", где 999 – содержимое связанного с ней тега.
Таким образом, полезная емкость кэш-памяти всегда меньше ее полной (физической) емкости, т.к. некоторая часть ячеек расходуется на создание тегов, совокупность которых так и называется "память тегов" (остальные ячейки образуют "память кэш-строк"). Следует заметить, что производители всегда указывают именно полезную, а не полную емкость кэш-памяти, поэтому, за память, "отъедаемую" тегами, можно не волноваться.
__Разрядность тегов определяется объемом кэшируемой памяти, вернее наоборот, максимально достижимый объем кэшируемой памяти ограничивается разрядностью тегов.
__Естественно, как только будет прочитан запрошенный процессором байт, кэш-контроллер тут же передаст его процессору.
Особенности кэш-подсистемы процессора AMD Athlon
Процессор AMD Athlon в целом ведет себя подобно своему предшественнику AMD K6, тем не менее, внутренняя архитектура его кэш-подсистемы претерпела значительные изменения. В частности, впервые за всю историю x86 процессоров в нем реализован эксклюзивный кэш второго уровня, эффективная емкость которого по заверениям разработчиков равна сумме размеров кэш-памяти обеих уровней, т.е. в данном случае: 64 + 256 = 320 Кб. Доверие – это прекрасно, но все-таки давайте попробуем прокатиться на этой машинке сами!
…ну и где же обещанные нам 320 Кб? Хорошо, пусть "ступенька", расположенная у отметки в ~257 Кб, вызвана конфликтом стека и обрабатываемых данных, но ведь тотальное падение производительности начинается уже с ~273 Кб, что много меньше ожидаемого (читай: заявленного разработчиками) значения!
достигая максимума насыщения на отметке в ~385 Кб.
Тем не менее, на участке от 273 Кб до 320 Кб время доступа растет не линейно, а подчиняется формуле 1/x, т.е. эксклюзивная архитектура все-таки смягчает падение производительности при выходе за границы кэша второго уровня. Во всяком случае, эффективный объем кэша второго уровня оказался не меньше, а даже чуть-чуть больше его физической емкости, в то время как аналогичный по размеру кэш процессора P-III начал "валится" уже на 194 Кб (см. рис. graph 3).
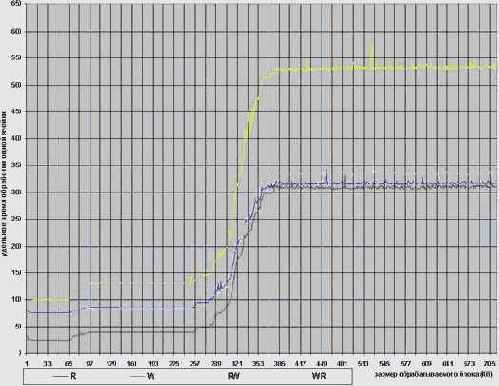
Рисунок 20 graph 2 Зависимость скорости обработки от размера блока на AMD Athlon
Особенности кэш-подсистемы процессоров P-II и P-III
Несмотря на свою в общем-то далеко не передовую inclusive–архитектуру, кэш-подсистема процессора P-II, а уж тем более его преемника P-III, всухую уделывает Athlon, значительно обходя его в производительности.
Благодаря своей 256-битной шине, процессор P-III может загружать 32-байтовый пакет данных из кэша второго уровня всего за один такт, против девяти тактов, которые тратит на это Athlon (т.к. при ширине шины в 64бита протяженности кэш-линеек составляет 64 байта, а кэш второго уровня работает по формуле 2-1-1-1-1-1-1-1, в сумме мы и получаем 9 тактов). Взгляните на рис. 3, – видите, кривая чтения (она выделена синим цветом) на всем протяжении остается идеально горизонтальной и "ступеньки" между кэшем первого и второго уровней на ней нет! Эффективный размер кэша перового уровня процессора P-III равен размеру кэша второго уровня, что составляет 256 Кб! Terrific!!! Правда, с записью памяти дела обстоят не так благоприятно и некоторое падение производительности при выходе за границы кэша первого уровня все же наблюдается, но оно так мало, что им можно безболезненно пренебречь.
Интересно другое. Характер изменения кривой записи памяти при выходе за пределы кэша второго уровня на P-II и P-III носит ярко выраженный нелинейный
характер. Вместо стремительного падения производительности, имеющей место на K6 и Athlon, здесь она убывает крайне медленно, как бы нехотя, достигая насыщения лишь при достижении 1 Мб отметки, что вчетверо превышает размеры кэша второго уровня. Не правда ли, очень здорово!
Здорово оно, может быть и здорово, но вот за счет чего этот выигрыш достигается? Официальная документация, увы, не дает прямой ответа на этот вопрос, а сторонние руководства позорно уходят в кусы, объясняя происходящее "особенностями буферизации". Что же это за особенности такие – пускай разбираются сами читатели! И разберемся!
Секрет (впрочем, какой это теперь секрет) фирмы Intel состоит в том, что при записи ячеек памяти, соответствующие им линейки загружаются в кэш второго уровня как эксклюзивные.
Остальные же процессоры ( в частности, уже упомянутые Athlon и K6), напротив, помечают эти линейки как модифицируемые. Не знаю, раздерет ли меня Intel на клочки, но я все-таки рискну не только пустить пыль в глаза, но и подробно разъясню все вышесказанное.
Итак, мысленно представим, как происходит процесс записи ячейки, отсутствующей в кэш-памяти первого уровня. Если ни одного свободного буфера записи нет (а при интенсивной записи памяти их и не будет), процессор вынужден загружать модифицируемую ячейку в кэш первого уровня. Он посылает сигнал кэшу второго уровня, который считывает 32 байтный блок памяти в одну из своих строк, присваивает ей атрибут "эксклюзивная" и передает ее копию кэшу первого уровня. Так продолжается до тех пор, пока обрабатываемый блок не превысит размеров кэша первого уровня и тогда процессор будет вынужден избавиться от наименее нужной строки, чтобы освободить место для новой. Поскольку все строки модифицированы, выбирается наиболее старя из них и отправляется в кэш второго уровня. Поскольку, в кэше второго уровня уже есть ее копия, он просто обновляет содержимое соответствующей ей линейки и изменяет атрибут "эксклюзивный" на "модифицируемый".
А теперь мы дождемся момента, когда кэш второго уровня будет полностью заполнен, но процессор предпримет попытку записи еще одной ячейки. Что происходит? Кэш первого уровня отправляет кэшу второго уровня сразу два запроса: запрос на загрузку новой порции данных и запрос на обновление вытесняемой кэш-линейки, чем серьезно его озадачивает, – ведь свободное место уже исчерпано. Ага, – говорит кэш второго уровня, – сейчас мы выкинем самое ненужное. А что у нас ненужное? Правильно, – эксклюзивные строки. Их удаление не требует предварительной выгрузки в основную память, а потому и обходится дешевле. Тем временем, пока кэш второго уровня загружает новую порцию данных из оперативной памяти, строка, вытесненная из кэша первого уровня содержится в специальном буфере и в дальнейшем записывается в основную память минуя кэш второго уровня.
Ключевой момент истории состоит в том, что вновь загруженная порция данных получает атрибут эксклюзивной, что делает ее кандидатом номер один на вытеснение. Постойте! Но ведь это означает, что при выходе за пределы кэша второго уровня, записываемые данные будут замещать одну и ту же кэш-строку, сохраняя ранее записанные строки в неприкосновенности! Это выгодно отличает P-II, P-III от процессоров K6 и Athlon, в обработка блока, не умещающегося в кэше второго уровня, приводит к последовательному замещению всех его строк.
Допустим, размер записываемых данных вдвое превышает емкость кэш-памяти второго уровня. Тогда в K6 и Athlon кэш будет крутиться полностью вхолостую, а на P-II и P-III только половина обращений вызовет промахи, а остальная благополучно сохранится в кэше. Впрочем, если говорить объективно, это не совсем так. Вследствие ограниченной ассоциативности кэша постоянным перезагрузкам подвернется не одна-единственная строка, а целый банк.
Теперь, в свете вновь открывшихся обстоятельств, становится ясен характер кривой, сопровождающий выход обрабатываемого блока за границы кэша второго уровня. Действительно, сохранение части кэшируемой памяти как бы оттягивает момент насыщения, скругляя острые углы графика записи. Более того полное насыщение вообще не наступает, т.к. при любом конечном размере обрабатываемого блока, сколь бы большим он ни был, сохраненные строки в той или иной мере повышают производительность. Другой вопрос, что с ростом соотношения эффективность такой стратегии стремится к нулю и если размер обрабатываемого блока превосходит емкость кэша в четыре или более раз, ей можно пренебречь.
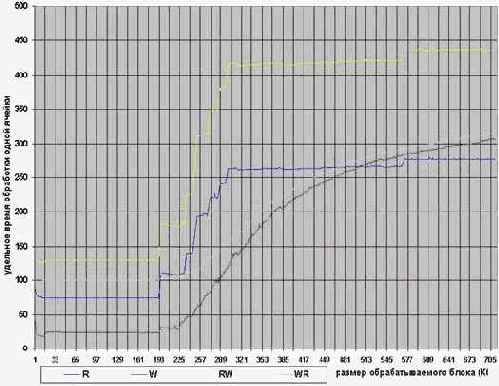
Рисунок 21 graph 3 Зависимость скорости обработки от размера блока на P-III
Чтение перед записью и запись перед чтением.
Операция записи ячейки с последующим ее чтением выполняется так же быстро, как и одиночная запись. Это не покажется удивительным, если вспомнить, что при промахе кэша первого уровня записываются данные временно сохраняются в буфере откуда они могут быть прочитаны в течение такта записи.
Другое дело – чтение с последующей записью. Тут, крути не крути, а при каждом промахе придется дожидаться пока данные не будут прочитаны из кэша второго уровня, в результате каждая операция требует по меньшей мере четырех дополнительных тактов. Измерения показывают, что так оно и есть.
На графике ??? изображены четыре кривые: ###синяя соответствует чтению тестируемого блока, фиолетовая – записи, желтая – чтению с последующей записью, а голубая – записью с последующим чтением.
Но вот ступенька пройдена и размер обрабатываемого блока становится таким большим, что не умещается в кэш-памяти второго уровня и мало-помалу начинает с нее "свешивается". График скоростного показателя чтения поднимается вверх и продолжает расти до тех пор, пока размер обрабатываемого блока не превысит емкости кэш-памяти первого уровня в 1.28 раза. Эта цифра хорошо согласуется с теоретическим значением – 1.25 (ассоциативность L2-кэша равна четырем). А вот три других графика ведут себя совсем не так, демонстрируя просто чудовищное падение производительности. Впрочем, этого и следовало ожидать – ведь промахи записи кэша второго уровня обходятся очень "дорого".
Особенности обработки двумерных массивов
Техника параллельной загрузки данных (подробно рассмотренная в первой части настоящей книги) весьма эффективный способ… отправить свою программу на кладбище. Подсистема памяти не так проста как кажется, и один неосторожный шаг способен разнести всю оптимизацию к черту. Но довольно лирики! Переходим к делу.
Допустим, у нас имеется здоровенный двухмерный массив, сумму ячеек которого и требуется подсчитать. Для определенности возьмем матрицу 512х512, состоящую из переменных типа int. Двухмерность массива порождает буриданову проблему: как вести подсчет– по строкам или по столбцам?
Подсчет по строкам фактически сводится к последовательному чтению памяти, а это (как мы помним) далеко не лучший способ обработки данных. Куда заманчивее читать массив по столбцам. Если ширина матрицы превышает длину пакетного цикла обмена, запросы к памяти генерируются при каждом
кэш-промахе (см. "Часть I.Оптимизация работы с памятью. Параллельная обработка данных"). Единственное условие – произведение столбцов на размер кэш-линии не должно превышать емкости кэш-памяти первого уровня.
Соблюдается ли это условие в данном случае? На первый взгляд как будто бы соблюдается. Смотрите: на P-III размер кэш-линеек составляет 32 байта, а размер кэш-памяти первого уровня – 16 Кб. В то же время: 512 x 32 = 16.384. Совпадают ли цифры? Совпадают! Хорошо, возьмем, например, AMD Athlon, имеющий 64 Кб кэш при длине линеек в 64 байт. Умножаем 512 на 64 – получаем 32 Кб, что с лихвой должно вместится в кэш. Но вместится ли? Сейчас проверим! Запустим на выполнение следующий пример:
#define N_ROW (512)
#define N_COL (512) // неоптимальное колю строк матр.
// поскольку оно кратно размеру
// кэш-банка и кэш используется
// _не_ полностью
/*----------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНАЯ ОБРАБОТКА МАССИВА ПО СТОЛБЦАМ
*
----------------------------------------------------------------------------*/
int FOR_COL(int (*foo)[N_COL])
{
int x, y;
int z = 0;
for (x = 0;x < N_ROW; x++)
{
for (y = 0; y < N_COL; y++)
z += foo[x][y];
}
return z;
}
/*----------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНАЯ ОБРАБОТКА МАССИВА ПО СТРОКАМ
*
----------------------------------------------------------------------------*/
int FOR_ROW(int (*foo)[N_COL])
{
int x, y;
int z = 0;
for (x = 0; x < N_COL; x++)
{
// внимание: если высота матрицы кратна размеру кэш-банка, то
// вследствии ограниченной ассоацитивности кэша его эффективная
// емкость значительно снизится и кэш-памяти может по просту
// не хватить, что приведет к постоянным промахам!
for (y = 0; y < N_ROW; y++)
z += foo[y][x];
}
return z;
}
Листинг 12 [Cache/column.big.c] Пример, демонстрирующий особенности обработки больших двухмерных массивов
Да как бы ни так! Мы совсем забыли про ассоциативность – поскольку, адреса читаемых ячеек кратны 4096, всего лишь четыре ячейки могут одновременно находится в кэше, но никак не 1024! Даже емкости кэша второго уровня для этих целей окажется недостаточно! Допустим, мы имеем, четырех ассоциативный 128 Кб L2-кэш. Каждый его банк способен хранить CACHE.SIZE/WAY/STEP.SIZE = 131.072/4/4096 == 32 таких ячеек. Следовательно, четыре банка разместят 32*4 = 128 ячеек. А у нас их аж 1024… Облом-с!
Сверхоперативная память будет крутиться полностью вхолостую, а величина кэш-промахов достигнет даже не 100%, а… 800% на P-II/P-III и 1.600% на AMD Athlon! Действительно, ведь в силу пакетного обмена, кэш-строки заполняются целиком, но только малая их часть оказывается реально востребована! В результате, данный код будет исполняется очень медленно.
Рисунок 31 graph 0x011 Зависимость времени обработки двухмерных массивов в зависимости от шага чтения.
Поскольку, обмен с кэшем и основной оперативной памятью осуществляется не отдельными ячейками, а пакетами достигающими в длину от 32 до 128 байт, при последовательной обработке ячеек время доступа к ним оказывается крайне неоднородным. Задержки возникают лишь при чтении первой ячейки пакета, а остальные ячейки пакета обрабатываются практически мгновенно.
Из этого в частности следует, что большие многомерные массивы (т.е. не умещающиеся в кэш-памяти первого, а тем более второго уровней) выгоднее обрабатывать не по столбцам, а по строкам. Массивы, целиком влезающие в кэш, можно обрабатывать как угодно – от этого хуже не будет.
На первый взгляд, программа column.big.c переставляет собой пример чрезвычайно высоко оптимизированного кода. Благодаря величие своего шага, первый проход цикла for y инициирует параллельную загрузку ячеек из основной оперативной памяти (или кэша второго уровня). Поскольку, размер обрабатываемых данных составляет всего лишь 1024*CACHE_LINE_SIZE == 32 Кб (что целиком умещается в кэш первого или на худой конец второго уровня), – может показаться, что последующие итерации цикла будут обрабатываться практически мгновенно, – ведь данные уже в кэше, а не в памяти!
Чтобы решить проблему, программу следует реорганизовать так:
int x,y,z;
int foo[1024][1024];
for (x=0;x<1024;x++)
{
for (y=0; y<1024;y++)
{
z=foo[x][y];
}
}
Листинг 13
Обрабатывая цикл не по столбцам, а по строкам, мы избавляемся от кэш-конфликтов и снижаем процент кэш-промахов до разумного минимума. Если хотите – мы даже можем рассчитать его поточнее. Несмотря на то, что массив foo, занимая 1024x1024x4 = 4 Мб памяти, намного превосходит и кэш первого, и кэш второго уровня, мы имеем всего лишь 12.5% промахов на P-II/P-III, а AMD Athlon и вовсе обходимся пактически без промахов– 6.25%! Согласитесь, что 6.25% это совсем не тоже самое, что и 1.600%!
Вот такая она разница между строками и столбцами!
В кэше второго уровня ячейка foo[1][0] так же имеет немного шансов сохранится. Пускай, емкости L2-кэша хватает с лихвой, но в многозадачной системе этот кэш приходится делить между множеством приложений – поскольку, первый проход цикла растянется на десятки тысяч тактов процессора, в течение этого времени не раз и не два произойдет переключение контекста и управление будет передано другим задачам. Если хотя бы одна из них интенсивно работает с памятью она может затереть таким трудом загруженные в L2-кэш строки массива foo, и – весь труд насмарку!
Поскольку, величина шага цикла for y превышает размер пакетного цикла обмена с памятью, в осуществляется параллельная загрузка ячеек
Смотрите, как все происходит: при попытке обращения к ячейке foo[0][0] кэш-контроллер, выяснив, что в кэше первого уровня она отсутствует, обращается к кэшу второго уровня. Там этой ячейки, скорее всего, тоже нет и приходится загружать полную 32-байтную строку из оперативной памяти, на что расходуется десятки тактов процессора.
Следующая ячейка – foo[1][0] – расположенная в соседней строке массива, отстоит от только считанной ячейки на 1024x4 байт, что много больше длины 32-байтной кэш-линии, поэтому она вновь загружается из оперативной памяти…
Наконец, первая колонка полностью обработана и наступает черед второй. Ячейки foo[1][0] уже не содержится в кэше. Почему? Ведь мы прочли всего четыре килобайта (1.024х4 = 4.096), что много меньше емкости L1-кэша? Если же реорганизовать цикл, читая его вот так: z=foo[x][y] скорость обработки многократно возрастет! Действительно, задержка при обращении к ячейке foo[0][0] компенсируется тем, что последующие восемь ячеек будут прочитаны практически мгновенно! Аналогично – foo[0][4] вызывает задержку на время подрузки данных из оперативной памяти, но каждая из последующих ячеек foo[0][5] foo[0][6] … foo[0][12] читается за один такт! В результате мы получаем практически семикратное ускорение – неплохо, правда?
Особое замечание о создании защитного кода на ассемблере
Защитные механизмы, бесспорно, предпочтительнее всего реализовывать на голом ассемблере, используя максимум трюков и извращений. Эффективность ассемблера здесь вторична, главное – максимально запутать взломщика. Компиляторы же генерируют достаточно предсказуемый код и почерк каждого из них профессиональным хакерам хорошо известен. Достоинства ассемблера в том, что он практически не ограничивает полет фантазии и позволяет воплощать в жизнь практически любые идеи. Полиморфный, шифрованный, самомодифицирующийся код, антиотладочные и антидизасемблерные приемы… этом список можно продолжать бесконечно. Целесообразность использования тех или иных защитных механизмов – тема другого разговора, здесь же мы будем обсуждать лишь пути их реализации.
Ассемблерные трюки – вообще больная тема, однако, следует различать трюк как таковой (оригинальная идея и/или нетрадиционный примем программирования) и недокументированные возможности
процессора и операционной системы. Трюки, при грамотном подходе к ним, вполне безобидны и никаких проблем не создают. Классический пример трюка – расшифровка программы одноразовым блокнотом, возвращаемым функцией rand. Поскольку, функция rand всегда возвращает одну и ту же последовательность, она идеально подходит для динамической шифровки/расшифровки программы. Если дизассемблер не сумеет распознать rand в откомпилированной программе, – хакер ногу сломит, пока не догадается: как устроена и работает такая защита. Какие проблемы может создать этот трюк? Совершенно верно, – никаких.
А вот пример "грязного хака", основанного на недокументированных возможностях: в Windows95 регион адресного пространства от 0xC0000000 до 0xF0000000, хранящий низкоуровневые компоненты системы, свободно доступен прикладным приложениям, что очень облегчает борьбу с отладчиками и всякими мониторами. Правда, под Window NT первая же попытка обращения к этой области приводит к генерации исключения с последующим закрытием приложения–нарушителя. В результате, конечный пользователь теряет возможность запускать защищенную программу под Windows NT.
Вот за это многие и не любят ассемблер. Но, позвольте, разве ж ассемблер виноват? Не используйте недокументированных особенностей (а если уж совсем невтерпеж, то используйте их с умом) – и проблем ни у кого не будет!
В последнее время, кстати, наметилась устойчивая тенденция к отказу от ассемблера даже в защитных механизмах. Действительно, многие трюки замечательно реализуются и на языках высокого уровня. В частности, динамическую расшифровку кода (равно как и исполнение кода в стеке) можно реализовать и на чистом Си/Си++, достаточно лишь получить указатель на функцию (Си это позволяет), после чего с ее содержимым можно делать все, что угодно. И вовсе не обязательно для этого спускаться на уровень голого ассемблера. Так же, язык высокого уровня облегчает написание полиморфных генераторов и виртуальных машин (машин Тьюринга, сетей Петри, стрелок Пирса и т.д.). Единственное, что нельзя на нем реализовать – так это самомодифицирующийся код. Вернее, можно, но с жесткой привязкой к конкретному компилятору (ибо необходимо знать: как и во что транслируется каждая строка), а подобная практика – дурной тон. Привязываться ни к чему и ни когда не стоит, к тому же трудозатраты при создании самомодифицирующегося кода на языке высокого уровня намного выше, чем на ассемблере.
Тем не менее, возможность создания защит на чистых Си/Си++ многих хакеров старого поколения просто корежит, – они и слышать об этом не хотят (автор, кстати, сам такой). Что поделаешь! Традиции и привычки – штучки упрямые. Ну, красиво программирование на голом ассемблере, понимаете? А создание защит непосредственно в машинных кодах вызывает ничем не передаваемое удовлетворение по своему эмоциональному накалу сравнимое разве что с оргазмом.
Это – программирование ради программирования, нацеленное не на конечный результат, а на сам процесс его достижения. Не могу удержать, чтобы не процитировать: "Для некоторых людей программирование является такой же внутренней потребностью, подобно тому, как коровы дают молоко, или писатели стремятся писать" Николай Безруков
Отказ от индикатора завершения
По возможности не используйте какой бы то ни было индикатор завершения для распознания конца данных (например, символ нуля для задания конца строки). Во-первых, это приводит к неопределенности в длине самих данных и количества памяти, необходимой для их размещения, в результате чего возникают ошибки типа "buff = malloc(strlen(Str))", которые с первого взгляда не всегда удается обнаружить. (Пояснение для начинающих разработчиков: правильный код должен выглядеть так: "buff = malloc(strlen(Str)+1)", поскольку, в длину строки, возвращаемой функцией srtlen, не входит завершающий ее ноль).
Во-вторых, если по каким-то причинам индикатор конца будет уничтожен, функция, работающая с этими данными, "забредет" совсем не в свой "лес".
В-третьих, такой подход приводит к крайне неэффективному подсчету объема памяти, занимаемого данным, - приходится их последовательно перебирать один за другим до тех пор пока не встретится символ конца, а, поскольку, по соображениям безопасности, при каждой операции контекции и присвоения необходимо проверять достаточно ли свободного пространства для ее завершения, очень важно оптимизировать этот процесс.
Значительно лучше явным образом указывать размер данных в отдельном поле (так, например, задается длина строк в компиляторах Turbo-Pascal и Delphi). Однако, такое решение не устраняет несоответствия размера данных и количества занимаемой ими памяти, поэтому, надежнее вообще отказаться от какого бы то ни было задания длины данных и всегда помещать их в буфер строго соответствующего размера.
Избавится от накладных расходов, связанных с необходимостью частных вызовов достаточно медленной функции realloc можно введением специального ключевого значения, обозначающего отсутствие данных. В частности, для строк сгодится тот же символ нуля, однако, теперь он будет иметь совсем другое значение – обозначать не конец строки, а отсутствие символа в данной позиции. Конец же строки определяется размером выделенного под нее буфера данных. Выделив буфер "под запас" и забив его "хвост" нулями, можно значительно сократить количество вызовов realloc.
Отображение физических DRAM-адресов на логические
С точки зрения процессора оперативная память представляется однородным массивом данных, доступ к ячейками которого осуществляется посредством 32-разрядных указателей. В тоже время адресное пространство физической оперативной памяти крайне неоднородно и делится на банки, адреса страниц и номера столбцов (а так же номера модулей памяти, если их установлено более одного). Согласованием интерфейсов оперативной памяти и процессора занимается чипсет, а сам процесс такого согласования называется трансляцией
(отображением) физических DRAM-адресов на логические процессорные адреса.
Конкретная схема трансляции зависит от и типа установленной памяти, и от конструктивных особенностей чипсета. Программист полностью абстрагирован от деталей технической реализации всей этой кухни и лишен возможности "потрогать" физическую оперативную память руками. А, собственно, зачем это? Какая разница в какой строке и в каком столбце находится ячейка, расположенная по такому-то процессорному адресу? Достаточно лишь знать, что эта ячейка существует, – вот и все. Что ж, абстрагирование от аппаратуры, – действительно великая вещь и отличный способ заставить программу работать на любом оборудовании, но… насколько эффективно она будет работать?
В главе "Оптимизация работы с памятью" будет показано, что обеспечить эффективную обработку больших массивов данных без учета архитектурных особенностей DRAM – невозможно. Как минимум мы должны иметь представление по какому именно физическому адресу происходит чтение/запись ячеек памяти.
К счастью, схема трансляции адресов в подавляющем большинстве случаев практически идентична (см. рис. 42). Младшие биты логического адреса представляют собой смещение ячейки относительно начала пакетного цикла обмена и никогда не передаются на шину. В зависимости от модели процессора длина пакетного цикла обмена колеблется от 32 байт (K6, P?II, P-III) до 64 байт (AMD Athlon) и даже до 128 байт (P-4). Соответственно, количество битов, отводимых под смещение внутри пакета различно и составляет на 4-, 5- и 6 битов на K6/P?II/P?III, Athlon и P-4 соответственно.
Следующая порция битов указывает на смещение ячейки внутри DRAM-страницы (или, другими словами говоря, представляет собой номер столбца). В зависимости от конструктивных особенностей микросхемы памяти длина DRAM-страниц может составлять 1-, 2,-, или 4 Кб, поэтому, количество бит, необходимых для ее адресации, различно. Но ведь разработчики чипсетов тоже люди и реализовывать несколько систем трансляции адресов им не в кайф! Большинство существующих чипсетов поддерживают модули памяти только с 2 Кб DRAM?страницами, что соответствует 7 битам, отводимых для их адресации. Более продвинутые чипсеты (в частности Intel 815) умеют обрабатывать страницы и большего размера, отображая старшие биты номера столбца в самый "конец" процессорного адреса. Таким образом, программная длина DRAM-страниц практически во всех системах равна 2 Кб, – и это обстоятельство еще не раз пригодится нам в будящем.
Следующие один или два бита отвечают за выбор банков памяти. Все модули памяти, емкость которых превышает 64 Мб имеют четыре DRAM-банка и потому отображают на логическое адресное пространство два бита (22=4).
Оставшиеся биты представляют собой номер DRAM-страницы и их количество напрямую зависит от емкости модуля памяти.

Рисунок 15 0х42 Типовая схема трансляция процессорных адресов в физические адреса DRAM-памяти
Пара слов в заключении
Многие считают использование самомодифицирующегося кода "дурным" примером программирования, обвиняя его в отсутствии переносимости, плохой совместимости с различными операционными системами, необходимости обязательных обращений к ассемблеру и т.д. С появлением Windows 95/Windows NT этот список пополнился еще одним умозаключением, дескать "самомодифицирующийся код – только для MS-DOS, в нормальных же операционных системах он невозможен (и поделом!)".
Как показывает настоящая статья, все эти притязания, мягко выражаясь, неверны. Другой вопрос – так ли необходим самомодифицирующийся код, и можно ли без него обойтись? Низкая эффективность существующих защит (обычно программы ломаются быстрее, чем успевают дойти до легального потребителя) и огромное количество программистов, стремящихся "топтанием клавиш" заработать себе на хлеб, свидетельствует в пользу необходимости усиления защитных механизмов любыми доступными средствами, в то числе и рассмотренным выше самомодифицирующимся кодом.
Параллельная обработка данных
Итак, обработка независимых данных выполняется намного быстрее, но насколько быстро она выполняется? Увы, если от относительных величин перейти к абсолютным цифрам,– весь восторг мгновенно улетучится и наступит глубокое уныние.
Наивысшая пропускная способность, достигаемая при линейном чтении независимых данных, составляет не более чем 40%-50% от завяленной пропускной способности данного типа памяти. И это притом, что подсистема памяти для линейного доступа как раз и оптимизирована, и хаотичное чтение ячеек происходит, по меньшей мере, на порядок медленнее. А что может быть быстрее линейного доступа? (Аналогичный вопрос: что может быть короче, чем путь по прямой). Вот с поиска ответов на такие вопросы и начинается проникновение в истинную сущность предмета обсуждения.
В обработке независимых данных есть одна тонкость. Попытка одновременного чтения двух смежных ячеек в подавляющем большинстве случаев инициирует один, а не два запроса к подсистеме памяти. Это не покажется удивительным, если вспомнить, что минимальной порцией обмена с памятью является не отнюдь не байт, а целый пакет, длина которого в зависимости от типа процессора варьируется от 32- до 128 байт.
Таким образом, линейное чтение независимых данных еще не обеспечивает их параллельной обработки (обстоятельство, о котором популярные руководства по оптимизации склонны умалчивать). Вернемся к нашей программе (см. листинг [Memory/dependence.c]). Вот процессору потребовалось узнать содержимое ячейки *(int *) ((int) p1 + a). Он формирует запрос и направляет его чипсету, а сам тем временем приступает к обработке следующей команды – x += *(int *)((int)p1 + a + 4). "Ага", – думает процессор, – зависимости по данным нет и это хорошо! Но, с другой стороны… эта ячейка и без того возвратится с предыдущим запрошенным блоком, и посылать еще один запрос нет необходимости (чипсет, сколько его ни подгоняй, он быстрее работать не будет). Что ж, придется отложить выполнение данной команды до лучших времен.
Так, что там у нас дальше? Следующая команда – x += *(int *)((int)p1 + a + 8)
тоже отправляется на "консервацию", поскольку пытается прочесть ячейку из уже запрошенного блока. В общем, до тех пор, пока чипсет не обработает вверенный ему запрос, процессор (при линейном чтении данных!) ничего не делает, а только "складирует". Затем, по мере готовности операндов, команды "размораживаются" и процессор завершает их выполнение.
…наконец процессору встречается команда, обращающаяся к ячейке, следующей за концом последнего запрошенного блока. "Эх", – вздыхает процессор, – "если бы она мне встретилась раньше, – я бы смог отправить чипсету сразу два запроса!".
Более эффективный алгоритм обработки данных выглядит так: в первом проходе цикла память читается с шагом 32 байта (или 64/128 байт, если программа оптимизируется исключительно под Athlon/P-4), что заставляет процессор генерировать запросы чипсету при каждом обращении к памяти. В результате, на шине постоянно присутствуют несколько перекрывающихся запросов/ответов, обрабатывающихся параллельно (ну, почти параллельно). Во втором проходе цикла считываются все остальные ячейки, адреса которых не кратны 32 байтам. Поскольку, на момент завершения первого прохода они уже находятся в кэше, обращение к ним не вызовет больших задержек (см. рис 39).
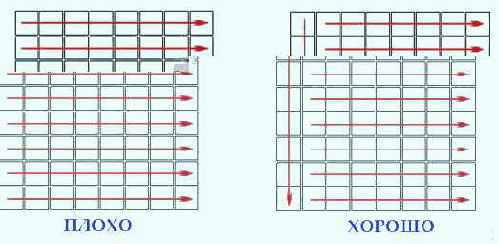
Рисунок 19 39. По возможности избегайте линейного чтения ячеек памяти. Лучше в первом проходе цикла читать ячейки с шагом, кратным размеру пакетного цикла обмена, а оставшиеся ячейки обрабатывать как обычно
Рассмотрим усовершенствованный вариант программы параллельного чтения независимых данных:
/* -----------------------------------------------------------------------
*
* измерение пропускной способности при параллельном чтении данных
*
----------------------------------------------------------------------- */
#define
BLOCK_SIZE (32*M) // размер обрабатываемого блока
#define
STEP_SIZE L1_CACHE_SIZE // размер обрабатываемого подблока
for (b=0; b < BLOCK_SIZE; b += STEP_SIZE)
{
// первый проход цикла, в котором осуществляется
// параллельная загрузка данных
for (a = b; a < (b + STEP_SIZE); a += 128)
{
// загружаем первую ячейку;
// поскольку ее пока нет в кэше,
// процессор отправляет чипсету
// запрос на ее чтение
x += *(int *)((int)p + a + 0);
// загружаем следующую ячейку
// поскольку зависимости по данным нет,
// процессор может выполнять эту команду,
// не дожидаясь результатов предыдущей
// но, поскольку процессор видит, что
// данная ячейка не возвратиться с
// только что запрошенным блоком,
// он направляет еще чипсету еще один запрос
// не дожидаясь завершения предыдущего
x += *(int *)((int)p + a + 32);
// аналогично, - теперь на шине уже три запроса!
x += *(int *)((int)p + a + 64);
// на шину отправляется четвертый запрос,
// причем, первый запрос возможно еще и
// не завершен
x += *(int *)((int)p + a + 96);
}
for (a = b; a < (b + STEP_SIZE); a += 32)
{
// следующую ячейку читать не надо
// т.к. она уже прочитана в первом цикле
// x += *(int *)((int)p + a + 0);
// а эти ячейки уже будут в кэше!
// и они смогут загрузиться быстро-быстро!
x += *(int *)((int)p + a + 4);
x += *(int *)((int)p + a + 8);
x += *(int *)((int)p + a + 12);
x += *(int *)((int)p + a + 16);
x += *(int *)((int)p + a + 20);
x += *(int *)((int)p + a + 24);
x += *(int *)((int)p + a + 28);
}
}
Листинг 10 [Memory/parallel.test.c] Фрагмент программы, реализующий алгоритм параллельного чтения памяти, позволяющий "разогнать" ее на максимальную пропускную способность
На P-III 733/133/100 такой трюк практически в полтора раза обгоняет алгоритм линейного чтения, достигая пропускной способности порядка 600 Mb/s, что лишь на 25% меньше теоретической пропускной способности (см. рис. graph 02). Еще лучший результат наблюдается на Athlon'е, всего на 20% не дотянувшим до идеала. Смотрите, латентность его неповоротливого чипсета практически полностью компенсирована, а сама система прямо-таки дышит мощью и летает, будто ей в вентилятор залетел шмель! И это притом, что сама тестовая программа написана на чистом Си без каких либо "хаков" и ассемблерных вставок! (То есть резерв для увеличения производительности еще есть!)
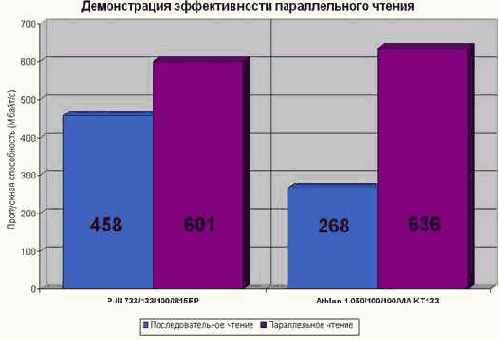
Рисунок 20 graph 0x002 Демонстрация эффективности параллельного чтения. На AMD Athlon 1050/100/100/VIA KT133 этот простой и элегантный трюк обеспечивает более чем двукратный прирост производительности. На P-III 733/133/100/I815EP выигрыш, правда, гораздо меньше – 20% – но все равно более чем ощутим
Переход на другой язык
В идеале, контроль за ошибками переполнения следовало бы поручить языку, сняв это бремя с плеч программиста. Достаточно запретить непосредственное обращение к массиву, заставив вместо этого пользоваться встроенными операторами языка, которые бы постоянно следили: происходит ли выход за установленные границы и если да, либо возвращали ошибку, либо динамически увеличивали размер массива.
Именно такой подход и был использован в Ада, Perl, Java и некоторых других языках. Но сферу его применения ограничивает производительность – постоянные проверки требуют значительных накладных расходов, в то время как отказ от них позволяет транслировать даже серию операций обращения к массиву в одну инструкцию процессора! Тем более, такие проверки налагают жесткие ограничения на математические операции с указателями (в общем случае требуют запретить их), а это в свою очередь не позволяет реализовывать многие эффективные алгоритмы.
Если в критических структурах (атомной энергетике, космонавтике) выбор между производительностью и защищенностью автоматически делается в пользу последней, в корпоративных, офисных и уж тем более бытовых приложениях наблюдается обратная ситуация. В лучшем случае речь может идти только о разумном компромиссе, но не более того! Покупать дополнительные мегабайты и мегагерцы ради одного лишь достижения надлежащего уровня безопасности и без всяких гарантий на отсутствие ошибок других типов, рядовой клиент ни сейчас, ни в отдаленном будущем не будет, как бы фирмы-производители его ни убеждали.
Тем более, что ни Ада, ни Perl, ни Java (т.е. языки, не отягощенные проблемами переполнения) принципиально не способны заменить Си\C++, не говоря уже об ассемблере! Разработчики оказываются зажатыми несовершенством используемого ими языка программирования с одной стороны, и невозможностью перехода на другой язык, с другой.
Даже если бы и появился язык, удовлетворяющий всем мыслимым требованиям, совокупная стоимость его изучения и переноса (переписывания с нуля) созданного программного обеспечения многократно бы превысила убытки от отсутствия в старом языке продвинутых средств контроля за ошибками.
Фирмы-производители вообще несут очень мало издержек за "ляпы" в своих продуктах и не особо одержимы идей их тотального устранения. В то же время, они заинтересованы без особых издержек свести их количество к минимуму, т.к. это улучшает покупаемость продукта и дает преимущество перед конкурентами.
Перемещение по тексту
Команда "End(Brief)" циклически перемещается к концу текущей линии, нижней строке в окне и, наконец, последней строке текста. Возможность быстрого перемещения к нижней строке окна, действительно, очень удобна, поэтому, имеет смысл назначить этой команде свою "горячую" клавишу. ("Tools à Customize à Keyboard à Category Edit à
End(Brief)").
Команда "Home(Brief)" очень похожа на предыдущую за тем исключением, что циклически перемещается не вниз, а вверх. По умолчанию ей так же не соответствует никакая "горячая" клавиша.
Комбинации <Ctrl-Стрелка вверх> и <Ctrl-Стрелка вниз> перемещают текст в окне соответственно вверх и вниз, сохраняя положение курсора, по крайней мере, до тех пор, пока он не достигнет последней строки окна. Это удобно при просмотре текста программы – чтобы увидеть следующую строку вам не обязательно через все окно гнать курсор вниз (вверх), как в обычном редакторе.
"Горячая" клавиша <F4> перемещает курсор к следующей строке, содержащий ошибку и отмечает ее черной стрелкой. Соответственно, <Shift-F4> перемещает курсор к предыдущей "ошибочной" строке.

Рисунок 4 0x04
Пишем собственный профилировщик
Какой смыл разрабатывать свой собственный профилировщик, если практически с каждым компилятором уже поставляется готовый? А если возможностей штатного профилировщика окажется недостаточно, то – пожалуйста – к вашим услугам AMD Code Analyst и Intel VTune.
К сожалению, штатный профилировщик Microsoft Visual Studio (как и многие другие подобные ему профилировщики) использует для измерений времени системный таймер, "чувствительности" которого явно не хватает для большинства наших целей. Профилировщик Intel VTune слишком "тяжел" и кроме того не бесплатен, а AMD Code Analyst не слишком удобен в работе и нет ни каких гарантий, что завтра за него не начнут просить деньги. Все это препятствует использованию перечисленных выше профилировщиков в качестве основных инструментов данной книги.
Предлагаемый автором DoCPU Clock, собственно, и профилировщиком язык назвать не поворачивается. Он не ищет горячие точки, не подсчитывает количество вызовов, более того, вообще не умеет работать с исполняемыми файлами. DoCPU Clock представляет собой более чем скромный набор макросов, предназначенных для непосредственно включения в исходный текст программы, и определяющих время выполнения профилируемых фрагментов. В рамках данной книги этих ограниченных возможностей оказывается вполне достаточно. Ведь все, что нам будет надо, – оценить влияние тех или иных оптимизирующих алгоритмов на производительность.
Планирование дистанции предвыборки
Поскольку, оперативная память – устройство медленное, загрузка кэш-линеек – дело долгое. Соответственно, предвыборку необходимо выполнять заблаговременно, с таким расчетом, чтобы, когда до обрабатываемых данных дойдет очередь, они уже находились в кэше.
При линейной обработке данных добиться этого очень просто, вот циклы – дело другое. Как быть, если время загрузки данных превышает продолжительность одной итерации? В примерах???2,4, приведенных выше, проблема решалась предвыборкой данных, обрабатываемых в следующей итерации цикла. Обратите внимание – именно следующей
итерации, а не через одну итерацию. Поэтому, лишь в первом проходе цикл исполняется неэффективно, а все последующие идут "на ура".
Как же это получается?! Весь если предвыборка успевает загружать данные за время выполнения предыдущей итерации, продолжительность загрузки не превышает продолжительности одной итерации, а раз так – зачем вообще потребовался этот сдвиг, ведь по идее данные должны успевать загружаться в течение текущего прохода цикла?
Ответ на вопрос кроется в механизме взаимодействия ядра процессора с подсистемой памяти. ### Подробно он рассматривался в первой части настоящей книги (см. "Устройство и принципы функционирования оперативной памяти. Взаимодействие памяти и процессора"), здесь же напомним читателю лишь основные моменты. ### Ввиду ограниченности объема журнальной статьи не будем останавливаться на этом подробно, а рассмотрим лишь основные моменты. В первую очередь нас будет интересовать поведение процессора при чтении ячеек памяти, отсутствующих в кэшах обоих уровней. Убедившись, что ни L1, ни в L2 кэше требуемой ячейки нет (и израсходовав на это один такт), процессор принимает решение получить недостающие данные из оперативной памяти. "Выплюнув" в адресную шину адрес ячейки, процессор, ценой еще нескольких тактов, передает его контроллеру памяти. Затем чипсет вычисляет номер столбца и номер строки ячейки, и смотрит: открыта ли соответствующая страница памяти или нет? Если страница действительно открыта, чипсет выставляет сигнал CAS и спустя 2-3 такта (в зависимости от величины задержки CAS, обусловленной качеством микросхемы памяти) на шине появляются долгожданные данные. (Если же требуемая строка закрыта, но максимально допустимое количество одновременно открытых строк еще не достигнуто, чипсет посылает микросхеме памяти сигнал RAS вместе с адресом строки и дает ей 2-3 такта на его "переваривание", затем посылается CAS и все происходит по сценарию описанному выше, в противном случае приходится терять еще такт на закрытие одной из страниц).
Контроллер памяти "проглатывает" первую порцию данных за один такт и с началом следующего такта передает ее заждавшемуся процессору, параллельно с этим "выдаивая" из микросхемы памяти вторую. Количество порций данных, загружаемых за один шинный цикл обращения к памяти, на разных процессорах различно и определяется размером линеек кэша второго уровня. В частности, P-II и K6, с 32-байтными кэш-линейками заполняют их четырьмя 64-битных порциями данных. Легко подсчитать, что полное время доступа к памяти требует от 10 до 12 тактов системной шины, но только 4 из них уходят на непосредственную передачу данных, а все остальное время шина свободна.
Однако если адрес следующей обрабатываемой ячейки известен заранее, процессор может отправить контроллеру очередной запрос, не дожидаясь завершения предыдущего. Конвейеризация позволяет скрыть латентность (начальную задержку) памяти, сократив время доступа к памяти с 10(12) тактов до 4 (см. рис 0х27). Правда, чтение первой ячейки будет по-прежнему требовать 10-12 тактов, но при циклической обработке данных этой задержкой можно пренебречь. Вот и ответ на вопрос – почему для эффективной предвыборки данных потребовался сдвиг на одну итерацию. Это необходимо для компенсации времени латентности (Tl), которая в данном случае существенно превосходит полезное время передачи данных (Tb).
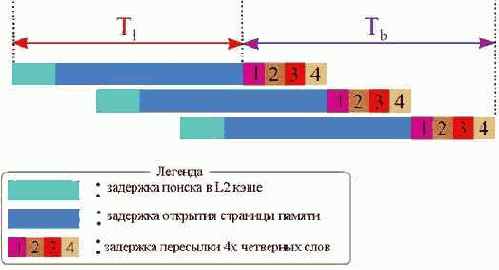
Рисунок 42 0х27 Демонстрация конвейеризации обмена с памятью.
Время выполнения цикла без использования предвыборки. В отсутствии предвыборки время выполнения цикла определяется суммой времени выполнения вычислительных инструкций цикла (Tc), времени латентности (Tl) и времени загрузки данных (Tb). Причем, во время выполнения вычислений системная шина простаивает, а во время загрузки данных, наоборот, вычислительный конвейер простаивает, а шина – работает. Причем, время доступа к памяти определяется не пропускной способностью шины, а латентностью подсистемы памяти. Шина же в лучшем случае нагружена на 15%-20% (см. рис. 0х028)
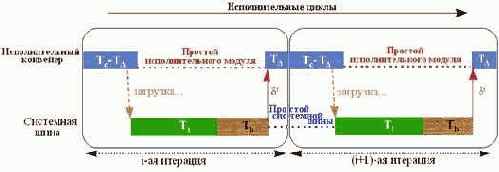
Рисунок 43 0х28 Исполнение цикла без использования предвыборки.
Время выполнения цикла в случае Tc>=Tl+Tb. Если время выполнения вычислительных инструкций цикла равно или превышает сумму времен латентности памяти и загрузки данных, упреждающая предвыборка эффективно распараллеливает работу системной шины с работой вычислительного конвейера (см. рис. 0х029).
Задержки доступа к памяти полностью маскируются, и время выполнения цикла определяется исключительно объемом вычислений, при этом производительность увеличивается в раз, т.е. в лучшем случае (при Tc=Tl+Tc) время выполнения цикла сокращает вдвое.
Минимальная дистанция предвыборки равна одной итерации, однако, если программа попадет на быстрый компьютер с медленной памятью (что типично для офисных и домашних компьютеров), запрошенные ячейки не успеют загрузиться за время выполнения предыдущей итераций. Это приведет к образованию "затора" на шине, вынужденному простою процессора и, как следствие, - тормозам.
Наилучший выход из ситуации – увеличить дистанцию предвыборки до двух-трех итераций. Да, мы теряем несколько первых проходов цикла, но при большом числе итераций, два-три прохода – это "капля в море"!
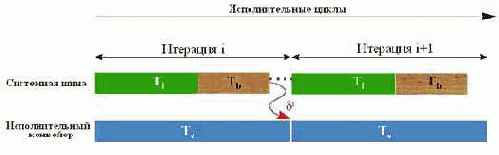
Рисунок 44 0х29 Исполнение цикла Tc>=Tl+Tb с дистанцией предвыборки в одну итерацию. Стрелкой с символом df показана зависимость по данным.
Время выполнения цикла в случае Tl+Tb > Tc> Tb. Если полное время доступа к памяти (т.е. сумма времени латентности и времени загрузки данных) превышает время выполнения вычислительных инструкций (Tc), но время выполнения вычислений в свою очередь превышает время загрузки данных, эффективное распараллеливание по-прежнему возможно! Необходимо лишь конвейеризовать запросы на загрузку данных, запрашивая очередную порцию данных до получения предыдущей. Это достигается увеличением дистанции предвыборки на несколько итераций, минимальное количество которых определяется по формуле:
(1),
где psd - Prefetch Scheduling Distance, – планируемая дистанция предвыборки, измеряемая в количестве итераций. Точно так, как и в предыдущем примере, в данном случае дистанцию предвыборки лучше взять с запасом, чем недобрать.
В худшем случае производительность увеличивается в два раза, а в среднем – в 4-5 раз (поскольку, типичная латентность памяти порядка 10 тактов, а время загрузки данных – 4 такта, то при Tc = Tb
получаем: ), причем загрузка системной шины достигает 80%-90% (в идеале – 100%). Великолепный результат, не так ли?
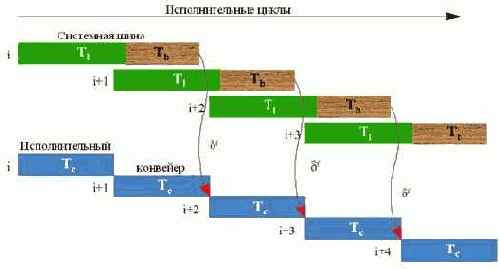
Рисунок 45 0х30 Исполнение цикла Tl+Tb > Tc> Tb. с дистанцией предвыборки в две итерации. Стрелкой с символом df показана зависимость по данным.
Время выполнения цикла в случае Tb > Tc. Наконец, если время загрузки данных (Tb) превышает время выполнения вычислительных инструкций цикла, полный параллелизм становится невозможен в принципе, – раз загрузка превышает продолжительность одной итерации, простой вычислительного конвейера неизбежен и никакая предвыборка тут не поможет. Тем не менее, предвыборка все же будет полезной, поскольку позволяет маскировать латентность памяти, что дает двух-трех кратный прирост производительности. Согласитесь – величина не малая. Оптимальная дистанция предвыборки определяется по формуле: (2).
Поскольку время выполнения цикла определяется исключительно скоростью загрузки данных (т.е. фактически частотой системной шины, загрузка которой в этом случае достигает 100%), излишне усердствовать над оптимизацией кода нет никакого смысла. Такая ситуация имеет место в частности, при копировании или сравнении блоков памяти. (Хотя, о оптимизация копирования – разговор особый. см. "Секреты копирования памяти или практическое применение новых команд процессоров Pentium-III и Pentium-4").
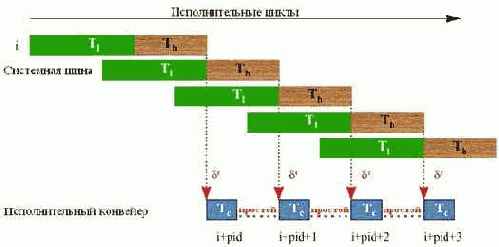
Рисунок 46 0х31 Исполнение цикла Tb > Tc. с дистанцией предвыборки в три итерации. Стрелкой с символом df показана зависимость по данным.
Практическое планирование предвыборки. Для вычисления оптимальной дистанции предвыборки необходимо знать: величину латентности памяти (Tl), время загрузки данных (Tb) и продолжительность выполнения одной итерации цикла (Tc). Поскольку, все три аргумента аппаратно–зависимы, приходится либо динамически
определять их значения в ходе выполнения программы, либо статически вычислять нижний предел дистанции предвыборки. Рассмотрим оба алгоритма подробнее.
Динамическое определение дает наивысший прирост производительности и достаточно просто реализуется. Один из возможных алгоритмов выглядит так: замеряв время выполнения первой итерации цикла (это можно сделать, например, посредством инструкции RDTSC), мы получаем сумму Tc+Tl+Tb. Затем, повторным выполнением этой же итерации, мы находим величину Tc (т.к. данные уже находятся в кэше время доступа к ним пренебрежительно мало). Разность этих двух величин даст сумму Tl+Tb, которой, вкупе с "чистой" Tc, вполне достаточно для вычисления формулы (???1).
Правда, определить "чистое" время Tb, необходимое для формулы (???2), таким способом довольно затруднительно, и лучше прибегнуть к алгоритму "вилки", суть которого заключается в следующем. Перебирая различные дистанции предвыборки и сравнения продолжительность соответствующих им итераций цикла, мы всего за несколько проходов найдем наиболее оптимальное значение, да не просто оптимальное, а самое-самое оптимальное, т.к. наилучшая дистанция предвыборки зачастую изменяется в процессе выполнения цикла. Особенно это характерно для разветвленных циклов, обрабатывающих неоднородные данные. К тому же динамический алгоритм определения дистанции предвыборки автоматически адоптируется под новые, еще не знакомые ему модели процессоров, в то время как статический анализ бессилен предвидеть их характеристики (Никто случайно не знает вычислительную скорость P-7?)
Статическое определение. В программах, рассчитанных на долговременное использование, статическое определение дистанции предвыборки нецелесообразно.
Никто не знает: какими будут процессоры через несколько лет, да и в настоящее время их характеристики повержены значительному разбросу. Если у CELERON-800 отношение частоты системной шины к частоте ядра равно 1:8, то у Pentium-4 1.300 оно лишь чуть-чуть не дотягивает 1:3. Вследствие этого соотношение у них будет сильно не одинаковым, и дистанция предвыборки, оптимальная для CELERON'а, окажется слишком малой для P-4, которому придется проставить, томительно ожидания загрузки очередной порции данных, в результате чего переход с CELETON на P-4 практически не увеличит производительности такой программы.
Поэтому, дистанцию предвыборки всегда планируйте с приличным запасом, по крайней мере, на 3-4 итерации больше необходимого минимума. Минимально необходимая дистанция предвыборки упрощенно вычисляется так:
(4)
где:
psd - Дистанция предвыборки (итераций цикла)
- Латентность памяти (тактов)
- Время загрузки кэш-строки (тактов)
- Количество предвыбираемых и сбрасываемых кэш-линий (штук)
CPI - Время выполнения одной инструкции (такты)
- Количество инструкций в одной итерации цикла (штуки)
В этой формуле почти все члены – неизвестные. Латентность памяти варьируется в очень широких пределах, поскольку определяется и типом самой памяти (SDRAM, DDR SDRAM, Rambus), и качеством чипов памяти (т.е. латентностью RAS и CAS), и "продвинутостью" чипсета, и, наконец, отношением частоты системной шины к частоте ядра процессора. Время загрузки кэш-строк пропорционально длине этих самых строк, которая составляет 32, 64 или 128 байт в зависимости от модели процессора (причем имеется ярко выраженная тенденция увеличения длины кэш-строк производителями).
Среднее время выполнения одной инструкции – вообще абстрактная величина, вроде среднего дохода граждан. Наряду с командами по трое сходящими с конвейера за один такт, некоторые (между прочим, достаточно многие) инструкции требуют десятков, а то и сотен тактов для своего выполнения! (В частности, целочисленное деление – не самая редкая операция, правда? – занимает от 50 до 70 тактов).
Таким образом, статическое планирование предвыборки в чем-то сродни гаданию на кофейной гуще. Но почему бы действительно не погадать? Intel приводит следующую эвристическую формулу, явно оговаривая ее ограниченность:
(5)
Подсчет количества инструкций в цикле () – очень интересный момент. Даже реализуя критические циклы на ассемблере (что для сегодняшнего дня вообще-то редкость), программист не может быть абсолютно уверен, что транслятор не впихнул туда чего-нибудь по собственной инициативе (например, NOP'ов для выравнивания). Что же тогда говорить о языках высокого уровня! Количество инструкций достоверно определяется лишь ручным их подсчетом в ассемблерном листинге (большинство компиляторов такие листинги генерировать умеют), однако, во-первых, это утомительное занятие придется проводить при всяком изменении текста программы. Во-вторых, если в цикле вызываются внешние функции (например, API-функции операционной системы) потребуется либо раздобыть исходные тексты ОС, либо дизассемблировать соответствующую функцию (но исходные тексты в большинстве случаев недоступны, а дизассемблер далеко не каждый умеет держать в руках). Наконец, в-третьих, полученный таким трудом результат все равно окажется неверным и ничуть не уступающим в точности киданию кости.
К счастью, интервал оптимальной дистанции предвыборки очень широк – даже увеличение минимального значения на порядок (!) в большинстве случаев снижает производительность не более чем на 10%-15% (а на многократно выполняющихся циклах – и того меньше). Поэтому, если скорость выполнения кода некритична, – динамическое определение дистанции предвыборки допустимо заменить статическим планированием, увеличив предвычисленный результат в несколько раз.
Хорошая идея – позволить пользователю задавать дистанцию предвыборки опционально. Чтобы не загромождать интерфейс и не смущать неопытных пользователей эти настойки можно запихнуть в реестр.
Планирование потоков данных
С проблемами, сопутствующими параллельной обработке нескольких блоков памяти (далее по тексту – потоков данных), мы уже столкнулись в предыдущем пункте. Здесь же этот вопрос будет рассмотрен более подробно. Итак, первое (и главное) правило – добиться, что бы потоки начинались с различных DRAM-банков (за TLB можно не беспокоиться, т.к. при параллельной обработке необходимые страницы уже будут там). Поскольку, большинство современных модулей памяти имеет четырех банковую организацию, очевидно, что работа с пятью и более потоками данных – нецелесообразна.
Однако это лишь вершина айсберга. Здесь, в зарослях тростника, притаилось немало тонкостей. Возьмем, например, руководство по чипсету VIAKT133. В нем черным по белому написано: "Supports maximum 16-bank interleave (i.e., 16 pages open simultaneously)… " – "Поддерживается чередование максимум 16-банков (т.е. 16 страниц могут быть открытыми одновременно)..." Означает ли это, что на чипсете VIA KT133 (и других, подобных ему, чипсетах) мы можем обрабатывать до 16 потоков данных? И да, и нет, причем скорее нет, чем да. Ключевое слово "максимум". Если воткнуть в системную плату всего один DIMM с четырех банковой организацией, то никакие конструкторские ухищрения не позволят чипсету удержать открытыми пять и более страниц DRAM-памяти. Поскольку микросхема памяти имеет всего лишь один сигнальный вывод RAS, то для открытия еще одной страницы в том же самом банке, этот сигнал придется дезактивировать, т.е. закрыть активную страницу.
Таким образом, крайне нежелательно обрабатывать более четырех потоков данных параллельно, в противном случае вы столкнетесь с проблемами производительности. Да, да, – хмыкнет читатель, – советовать что-либо не делать – проще всего. Гораздо сложнее найти решение как именно это делать! Положим, нам необходимо
обрабатывать более четырех потоков данных одновременно, причем, расплачиваться производительностью за постоянные открытия/закрытия DRAM-страниц мы категорически не хотим.
Тупик? Вылезаем, мы приехали? Вовсе нет!
Первое, что приходит на ум, – перейти на оперативную память типа RDRAM. В сочетании с чипсетом Intel 850 это обеспечит восемь реально открытых страниц, а это – восемь потоков данных! Удовлетворяет вас такое решение? В общем-то, да, но далеко не во всех случаях. RDRAM на сегодняшний день (точнее, момент написания этих строк – июнь 2002 года для справки) – не самый дешевый и распространенный тип памяти.
На самом деле, даже на обычной SDRAM памяти можно обрабатывать практически неограниченное
количество потоков данных, ничем не расплачиваясь взамен. Ведь никто не требует обрабатываемые именно физические
потоки. Вот и давайте, создав один физический поток, разобьем его на несколько логических (виртуальных) потоков или, другими словами говоря, используем interleave-трансляцию адресов. Тогда между адресами логических и физического потока будет установлено следующее соответствие:
p[N][a] == a*MAX_N + N /* 1 */
P[a] == a mod MAX_N /* 2 */
где:
p – массив указателей на адреса начала логических потоков,
P – указатель на адрес начала физического потока,
N – индекс логического потока,
а – индекс элемента логического потока N,
MAX_N – количество логических потоков,
"Живой" пример interleave–трансляции изображен на рис. 35. Смотрите, до оптимизации у нас было два обособленных блока памяти a) и b), каждый из которых хранил восемь ячеек памяти, обозначенных a0, a1…a7 и b0, b1…b7 соответственно. В оптимизированном варианте программы эти два блока объедены в один непрерывный блок, составленный из шестнадцати чередующихся ячеек блоков а и b, – a0, b0, a1, b1….a7, b7. Теперь, при параллельной обработке логических потоков a и b запрашиваемые данные сливаются в один физический поток, что: во-первых, позволяет избежать постоянного открытия/закрытия DRAM-страниц; во-вторых, гарантирует, что смежные ячейки потоков а и b не попадут на различные страницы одного и того же DRAM-банка, находящегося в момент обращения на регенерации.
И, в-третьих, облегчает работу системе аппаратной предвыборке (если таковая имеется), поскольку большинство таких систем оптимизированы всего под один поток (это легче реализовать, да и увеличение пакетного цикла обмена с памятью эффективно лишь при последовательном обращении к ней).
Причем, заметьте, все эти блага достаются практически даром и не слишком "утяжеляют" алгоритм. Правда, тут есть одна тонкость. Поскольку, переход от физического адреса потока к логическому, неизбежен без взятия остатка, то следует подумать: как избавиться от машинной команды DIV, выполняющей целочисленное деление. Дело в том, что деление – очень медленная операция, по времени приблизительно сопоставимая с закрытием одной DRAM-страницы. Если количество потоков соответствует степени двойки, то взятие остатка можно осуществить и быстрыми битовыми операциями. Другой путь – заменить взятие остатка умножением (см. ….).

Рисунок 30 0x35. Виртуализация потоков данных. Несколько исходных потоков (слева) сливаются в один физический
поток, сконструированный по принципу чередования адресов, что фактически равносильно его расщеплению на два логических
потока
Теперь давайте воочию убедимся насколько эффективной может быть оптимизация потоков при большом их числе. Для этого напишем следующую несложную программу и посмотрим на ее результат.
#define BLOCK_SIZE (2*M) // макс. объем виртуального потока
#define MAX_N_DST 16 // макс. кол-во виртуальных потоков данных
#define MAIL_ROOL(a) for(a = 2; a <= MAX_N_DST; a++)
/* ^^^^^^^ начинаем с двух виртуальных потоков */
int a, b, r, x=0;
int *p, *px[MAX_N_DST];
// шапка
printf("N DATA STREAM"); MAIL_ROOL(a) printf("\t%d",a);printf("\n");
/* -----------------------------------------------------------------------
*
* обработка потоков классическим (не оптимизированным) способом
*
------------------------------------------------------------------------ */
// выделяем память всем потокам
for (a = 0; a < MAX_N_DST; a++) px[a] = (int *) _malloc32(BLOCK_SIZE);
printf("CLASSIC");
MAIL_ROOL(r)
{
A_BEGIN(0) /* начало замера времени выполнения */
for(a = 0; a < BLOCK_SIZE; a += sizeof(int))
for(b = 0; b < r; b++)
x += *(int *)((int)px[b] + a );
// перебор всех потоков один за другим
// причем, как легко убедиться, ячейки
// всех потоков находятся в различных
// страницах DRAM, поэтому при обработке
// более четырех потоков, DRAM страницы
// будут постоянно закрываться/открываться
// снижая тем самым производительность
// ВНИМАНИЕ! в данном случае циклы a и b
// в принципе, возможно обменять местами,
// увеличив тем самым производительность,
// но мы же договорились обрабатывать
// потоки _параллельно_
A_END(0) /* конец замера времени выполнения */
printf("\t%d",Ax_GET(0)); // вывод времени обработки потока
} printf("\n"); /* end for */
/* -----------------------------------------------------------------------
*
* оптимизированная обработка виртуальных потоков
*
------------------------------------------------------------------------ */
// выделяем память физическому потоку
p = (int*) _malloc32(BLOCK_SIZE*MAX_N_DST);
printf("OPTIMIZED");
MAIL_ROOL(r)
{
A_BEGIN(1) /* начало замера времени выполнения */
for(a = 0; a < BLOCK_SIZE * r; a += (sizeof(int)*r))
// что изменилось? Смотрите, ^^^ - шаг приращения ^^^
// теперь равен кол-ву виртуальных потоков
for(b = 0; b < r; b++)
x += *(int *)((int)p + a + b*sizeof(int));
// теперь ячейки всех потоков расположены _рядом_
// поэтому, время их обработки - минимально
A_END(1) /* конец замера времени выполнения */
printf("\t%d",Ax_GET(1)); // вывод времени обработки потока
} printf("\n"); /* end for */
Листинг 20 [Memory/stream.virtual.c] Фрагмент программы, демонстрирующий эффективность виртуализации потоков в зависимости от их числа
Ого! Нет, конечно, мы догадывались, что оптимизирующий вариант обгонит классический, но кто же мог представить: насколько
он его обгонит! (см. рис. 13, 14). Вообще-то, на P-III 733/133/100/I815EP/2x4 вплоть до четырех потоков (максимально возможного количества одновременно открытых DRAM-страниц), оптимизированный вариант заметно отставал от не оптимизированного. Но уже на пяти потоках оба варианта сравнялись в скорости, а дальше… дальше с добавлением каждого нового потока время работы не оптимизированного варианта стало стремительно взлетать вверх. А у оптимизированного, напротив, – росло практически линейно (небольшие осцилляции объясняются особенностями кэш-подсистемы, о которых мы поговорим чуть позже см. "Кэш"). Так, уже на шестнадцати потоках (вполне реальная величина для типичных вычислительных задач), оптимизация дала более чем трехкратный выигрыш в скорости! И все это – повторяюсь, – без значительных изменений базового алгоритма. Оптимизацию потоков необязательно закладывать на этапе проектирования программы, – это можно сделать в любое удобное для разработчика время. К тому же, это далеко не предел производительности! Быстродействие программы можно значительно увеличить, если использовать параллельную обработку данных (см. "Параллельная обработка данных").

Рисунок 31 graph 13 Демонстрация эффективности виртуализации потоков данных на системе P-III 733/133/100/I815EP/2x4. Уже на 16 потоках оптимизация дает более чем трехкратный выигрыш
А вот и тесты системы AMD Athlon 1050/100/100/VIA KT133/4x4 (см. рис. graph 14). Забавно, но в данном случае оптимизированный вариант значительно обогнал не оптимизированный во всех случаях, даже при обработке всего двух потоков. Как же такое могло произойти? Помниться, документация обещала аж 16 одновременно открытых страниц, а на практике "сваливалась" всего лишь на двух. Верно, было нам такое обещано, но ведь в то же самое время утверждалось, что: "Four cache lines (32 quad words) of CPU to DRAM read prefetch buffers" – "Буфер предварительной выборки из DRAM, размером в четыре кэш-линии (32 четверых слова) центрального процессора [256 байт – КК]". Для уменьшения латентности инженеры из VIA решились на весьма ответственный шаг – осуществление упреждающего чтения из оперативной памяти. Алгоритм предвыборки должен уметь распознавать регулярные шаблоны обращения к данным и на их основе с высокой вероятностью предсказывать, к каким именно ячейкам произойдет следующее обращение. В противном случае от предвыборки будут одни убытки, – ведь в момент чтения оперативная память недоступна и вместо уменьшения латентности мы многократно увеличим ее!
К сожалению, документация вообще ничего не говорит о сценарии предвыборки, но ведь никто не запрещает нам догадываться, правда? Судя по всему, алгоритм упреждающего чтения в KT133 даже и не пытается распознать стратегию обращения к памяти, а просто загружает последующие 32 четверных слова при обращении ко всякой ячейке. Как следствие, – при работе с несколькими потоками данных содержимое буфера предвыборки будет вытесняться прежде, чем к нему произойдет реальное обращение и… "упрежденные" данные окажутся "упреждены" вхолостую. Отсюда и снижение производительности.
Поэтому, на чипсете VIA KT133 ( и подобных ему) крайне не рекомендуется работать более чем с одним физическом потоком данных. Причем, выигрыш в оптимизации даже превосходит систему на базе P-III/I815, – уже при 10 потоках наблюдается более чем пятикратный выигрыш! Не правда ли, VIA KT133 – хороший чипсет?
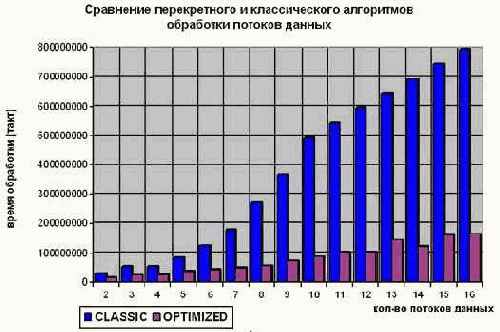
Рисунок 32 graph 14 Демонстрация эффективности виртуализации потоков данных на системе P-III/I815EP/2x4 AMD Athlon/VIA KT133/4x4
Особые случаи виртуализации потоков
Однако на этом сюрпризы не заканчиваются. Все что мы видим – верхушка айсберга. А если копнуть в глубь? Вот, например, как вы думаете: на каком минимальном расстоянии потоки данных могут располагаться друг от друга? Здравый смысл подсказывает: чем ближе, – тем лучше. А вот как бы не так! Особенности буферизации некоторых чипсетов (попросту говоря: криво реализованный механизм буферизации и/или неинтеллектуальной предвыборки) способен вызывать значительное снижение производительности, если происходит попеременное обращение к "близким" (с точки зрения чипсета) ячейкам памяти. Рассмотрим следующий пример:
for(a=0; a<BLOCK_SIZE; a+=STEP_FACTOR)
{
x += *(int *)((int)p + a );
y += *(int *)((int)p + a + DELTA_SIZE + STEP_FACTOR/2 );
}
Листинг 21 Пример неэффективного кода, не учитывающего особенности буферизации некоторых чипсетов
На системе Intel P-III 733/133/100/I815EP/2*4 время обработки блока практически не зависит от величины расстояния между потоками (DELTA_SIZE), естественно, если при этом не происходит постоянного попадания в один и тот же банк, но эту проблему мы уже обсудили (см. "Стратегия распределения данных по DRAM-банкам"). Казалось бы, какие тут могут быть сюрпризы? А вот взгляните на верхнюю кривую графика graph 12, иллюстрирующую поведение системы AMD Athlon 1050/100/100/VIA KT133/4 х 4. Оказывается, параллельная обработка данных, расположенных на расстоянии менее 512 байт друг от друга крайне невыгодна и несет чуть ли не двукратные издержки быстродействия.
Ох, уж эта система предвыборки в чипсете KT133! Конечно, можно просто заявить: "Используйте Intel (Intel – это рулез) и у вас не будет никаких проблем", но разработчик, заботящийся о своих клиентах, не должен ограничивать свободу выбора поставщика. Нравится кому-то VIA? – Да ради Бога! – Мы просто сместим начало каждого логического потока на 512 байт относительно предыдущего! Если количество требуемых потоков невелико, то с потерей нескольких килобайт можно и смириться, в противном случае возникнут попадания в регенерируемые банки и, – как следствие, – упадает производительность. Есть ли выход? Увы, общих решений нет… Правда, можно усложнить механизм трансляции адресов, расположив потоки приблизительно следующим образом: p0, 512 + p1, p2, 512 + p3…. тогда, при условии что потоки обрабатываются в строгой очередности, каждое обращение будет осуществляться без накладных расходов. Но что произойдет, если придется попеременно обращаться к данным потоков p1 и p3? Правильно – тормоза. Чтобы их избежать вам придется "заточить" механизм трансляции адресов потоков под алгоритм их обработки или… или вообще отказаться от оптимизации под VIA.

Рисунок 33 graph 12 Демонстрация особенностей механизма буферизации на чипсете VIA KT133. Смотрите, при узком "зазоре" между виртуальными потоками время их обработке чудовищно возрастает
Хорошо, с минимальным расстоянием мы разобрались. А существует ли максимально
разумное расстояние между потоками? Да, существует. И равно оно, как не трудно догадаться, – (N?1)*c /* на самом деле – даже (N?2)*c при хаотичной обработке блоков, но грамотным планированием потоков этой проблемы легко избежать */ Отсюда следует, что в один физический поток можно вместить не более чем: (N?1)*c/sizeof(element) логических потоков, где sizeof(element) – размер элементов потока. Так, для массивов, состоящих из элементов типа _int32, максимально разумное количество логических потоков равно: (4?1)*2048/4 == 1.536.
Не правда ли, это число более чем достаточно для всех – мыслимых и не мыслимых – задач?
Однако при этом максимально разумное количество физических потоков равно… одному. Ведь все DRAM-банки уже задействованы и при обращении ко второму физическому потоку никто не гарантирует, что мы не попадаем в регенерирующийся банк. Впрочем, тут все зависит от алгоритма работы с потоками, – вполне возможно добиться согласованной работы и четырех физических потоков, каждый из которых содержит по полторы тысячи логических. Но, постойте, сколько же это всего потоков получается? Шесть тысяч сто сорок четыре?! Трудно представить себе задачу, реально нуждающуюся в таком количестве потоков. Даже если это вычислительный кластер какой… Хотя, автору доводилось сталкиваться и с большим количеством параллельно обрабатываемых блоков данных – в системе, моделирующей движения звезд в галактиках, и пытающейся тем самым поближе подобраться к загадочной "темной материи", но это уже тема другого разговора… На персональных компьютерах пока подобные процессы не моделируют.
"Подводные камни" перемещаемого кода
При разработке кода, выполняющегося в стеке, следует учитывать, что в операционных системах Windows 9x, Windows NT и Windows 2000 местоположение стека различно, и, чтобы сохранить работоспособность при переходе от одной системы к другой, код должен быть безразличен к адресу, по которому он будет загружен. Такой код называют перемещаемым,
и в его создании нет ничего сложного, достаточно следовать нескольким простым соглашениям – вот и все.
Замечательно, что у микропроцессоров серии Intel 80x86 все короткие переходы (short jump) и близкие вызовы (near call) относительны, т.е. содержат не линейный целевой адрес, а разницу целевого адреса и адреса следующей выполняемой инструкции. Это значительно упрощает создание перемещаемого кода, но вместе с этим накладывает на него некоторые ограничения.
Что произойдет, если следующую функцию "void Demo() { printf("Demo\n");}" скопировать в стек и передать ей управление? Поскольку, инструкция call, вызывающая функцию pritnf, "переехала" на новое место, разница адресов вызываемой функции и следующей за call
инструкции станет совсем иной, и управление получит отнюдь не printf, а не имеющий к ней никакого отношения код! Вероятнее всего им окажется "мусор", порождающий исключение с последующим аварийным закрытием приложения.
Программируя на ассемблере, такое ограничение можно легко обойти, используя регистровую адресацию. Перемещаемый вызов функции printf упрощенно может выглядеть, например, так:"lea eax, printf\ncall eax." В регистр eax (или любой другой регистр общего назначения) заносится абсолютный линейный, а не относительный адрес и, независимо от положения инструкции call, управление будет передано функции printf, а не чему-то еще.
Однако такой подход требует значения ассемблера, поддержки компилятором ассемблерных вставок, и не очень-то нравится прикладным программистам, не интересующихся командами и устройством микропроцессора.
Для решения данной задачи исключительно средствами языка высокого уровня, - необходимо передать стековой функции указатели на вызываемые ее функции как аргументы.
Это несколько неудобно, но более короткого пути, по-видимому, не существует. Простейшая программа, иллюстрирующая копирование и выполнение функций в стеке, приведена в листинге 2.
void Demo(int (*_printf) (const char *,...) )
{
_printf("Hello, Word!\n");
return;
}
int main(int argc, char* argv[])
{
char buff[1000];
int (*_printf) (const char *,...);
int (*_main) (int, char **);
void (*_Demo) (int (*) (const char *,...));
_printf=printf;
int func_len = (unsigned int) _main - (unsigned int) _Demo;
for (int a=0;a<func_len;a++)
buff[a]= ((char *) _Demo)[a];
_Demo = (void (*) (int (*) (const char *,...))) &buff[0];
_Demo(_printf);
return
0;
}
Листинг 3 Программа, иллюстрирующая копирование и выполнение функции в стеке
Поиск
Команда "FindBackwardDlg" открывает диалоговое окно "Find", автоматически устанавливая обратное направление поиска строки. По умолчанию она не связана ни с какой "горячей" клавишей и назначить ее вы должны самостоятельно ("Tools à Customize à Keyboard à Category Edit à FindBackwardDlg").
Соответственно, команда "FindForwardDlg" открывает окно "Find", автоматически устанавливая прямое направление поиска. Штатный вызов диалога "Find" комбинацией <Ctrl-F> сохраняет последнее используемое направление.
Команды "FindRegExpr" и "FindRegExprPrev" открывают диалоговое окно "Find" автоматически устанавливая галочку "Поиск регулярных выражений", причем, первая из них задает прямое, а вторая – обратное направление поиска.
"Горячая" клавиша <F3> повторяет поиск предыдущей подстроки не вызывая диалог "Find", что намного быстрее.
Еще удобнее комбинация <Ctrl-F3>, которая ищет следующее вхождение выделенного текста. Т.е. вместо того, чтобы вводить искомую подстроку в диалог "Find" достаточно выделить ее и нажать <Ctrl-F3>. Соответственно, <Shift-Ctrl-F3> ищет следующее вхождение выделенного текста в обратном направлении.
Пара "горячих" клавиш <Ctrl-]>
и <Ctrl-Shift-]> перемещают курсор к следующей или предыдущей парной скобке соответственно. Это чрезвычайно полезно при разборе "монтроузных" выражений. Допустим, у нас имеется выражение "(((A) + (B)) + (C))" и необходимо найти пару второй слева скобке. Подводим к ней курсор, нажимаем <Ctrl-]> и… вот она, третья скобка справа! Соответственно, <Shift-Ctrl-]> возвратит нас на исходную позицию назад. Таким образом, проверка корректности вложения скобок из рутинного труда превращается в приятное развлечение.
Команды "LevelUp" и "LevelDown" очень похожи на предыдущие, но, во-первых, не требуют, чтобы курсор находился на скобке, а, во-вторых, не имеют собственных горячих клавиш.
На мой взгляд, это несправедливо и нелогично, т.к. они намного удобнее в работе!
Команды "LevelCutToEnd" и "LevelCutToStart" вырезают в буфер обмена тело выражения до следующей или предыдущей парной скобки соответственно. Если же вам надо не вырезать, а копировать, то можно прибегнуть к небольшой хитрости – вырезать текст и тут же выполнить откат (Undo). Фокус в том, что откат не затрагивает буфер обмена, но восстанавливает удаленный текст. Как нетрудно догадаться, обе команды "горячими" клавишами не обременены, и назначать их придется самостоятельно.
Рисунок 2 0х03 Поиск парных скобок
"Горячая" клавиша <Ctrl-D> перемещает курсор в "Find Tools" – ниспадающий бокс, расположенный на панели инструментов и сохраняющий несколько последних шаблонов поиска (см. рис. 3). Конечно, по нему можно кликнуть и мышкой, но клавиатура позволит сделать это быстрее, без отрыва рук от производства!
Рисунок 3 0х02 Переход в окно "Find Tools"
Поиск уязвимых программ
Приемы, предложенные в разделе "Предотвращение ошибок переполнения", хорошо использовать при создании новых программ, а внедрять их в уже существующие и более или менее устойчиво работающие продукты – бессмысленно. Но ведь даже отлаженное и проверенное временем приложение не застраховано от наличия ошибок переполнения, которые годами могут спать, пока не будут кем-то обнаружены.
Самый простой и наиболее распространенный метод поиска уязвимостей заключается в методичном переборе всех возможных длин входных данных. Как правило, такая операция осуществляется не в ручную, а специальными автоматизированными средствами. Но таким способом обнаруживаются далеко не все ошибки переполнения! Наглядной демонстрацией этого утверждения служит следующая программа:
int file(char *buff)
{
char *p;
int a=0;
char proto[10];
p=strchr(&buff[0],':');
if (p)
{
for (;a!=(p-&buff[0]);a++) proto[a]=buff[a];
proto[a]=0;
if (strcmp(&proto[0],"file")) return 0;
else
WinExec(p+3,SW_SHOW);
}
else WinExec(&buff[0],SW_SHOW);
return 1;
}
main(int argc,char **argv)
{
if (argc>1) file(&argv[1][0]);
}
Листинг 1 Пример, демонстрирующий ошибку переполнения буферов
Она запускает файл, имя которого указано в командной строке. Попытка вызвать переполнение вводом строк различной длины, скорее всего, ни к чему не приведет. Но даже беглый анализ исходного кода позволит обнаружить ошибку, допущенную разработчиком.
Если в имени файла присутствует символ “:”, программа полагает, что имя записано в формате “протокол://путь к файлу/имя файла”, и пытается выяснить какой именно протокол был указан. При этом она копирует название протокола в буфер фиксированного размера, полагая, что при нормальном ходе вещей его хватит для вмещения имени любого протокола. Но если ввести строку наподобие “ZZZZZZZZZZZZZZZZZZZZZZ:”, произойдет переполнение буфера со всеми вытекающими отсюда последствиями.
Приведенный пример относится к одним из самых простых. На практике нередко встречаются и более коварные ошибки, проявляющиеся лишь при стечении множества маловероятных самих по себе обстоятельств. Обнаружить подобные уязвимости одним лишь перебором входных данных невозможно (тем не менее, даже такой поиск позволяет выявить огромное число ошибок в существующих приложениях).
Значительно лучший результат дает анализ исходных текстов программы. Чаще всего ошибки переполнения возникают вследствие путаницы между длинами и индексами массивов, выполнения операций сравнения до модификации переменной, небрежного обращения с условиями выхода из цикла, злоупотребления операторами "++" и "—", молчаливого ожидания символа завершения и т.д.
Например, конструкция “buff[strlen(str)-1]=0”, удаляющая символ возврата каретки, стоящий в конце строки, "спотыкаться" на строках нулевой длины, затирая при этом байт, предшествующий началу буфера.
Не менее опасна ошибка, допущенная в следующем фрагменте:
// …
fgets(&buff[0], MAX_STR_SIZE, stdin);
while(buff[p]!='\n') p++;
buff[p]=0;
// …
На первый взгляд все работает нормально, но если пользователь введет строку равную или превышающую MAX_STR_SIZE, функция fgets
автоматически отбросит ее хвост, вместе с символом возврата каретки. В результате этого цикл while выйдет за пределы сканируемого буфера и залезет в совсем не принадлежащую ему область памяти!
Так же часты ошибки, возникающие при преобразовании знаковых типов переменных в беззнаковые и наоборот. Классический пример такой ошибки – атака teardrop, возникающая при сборке TCP пакетов, один из которых находится целиков внутри другого. Отрицательное смещение конца второго пакета относительно конца первого, будучи преобразованным в беззнаковый тип, становится очень большим числом и выскакивает далеко за пределы отведенного ему буфера. Огромное число операционных систем, подверженных атаке teardrop наглядно демонстрирует каким осторожным следует быть при преобразовании типов переменных, и без особой необходимости такие преобразования и вовсе не следует проводить!
Вообще же, поиск ошибок – дело неблагодарное и чрезвычайно осложненное психологической инерцией мышления – программист подсознательно исключает из проверки те значения, которые противоречат "логике" и "здравому смыслу", но тем не менее могут встречаться на практике. Поэтому, легче решать эту задачу с обратного конца: сначала определить какие значения каждой переменной приводят к ненормальной работе кода (т.е. как бы смотреть на программу глазами взломщика), а уж потом выяснить выполняется ли проверка на такие значения или нет.
Особняком стоят проблемы многопоточных приложений и ошибки их синхронизации. Однопоточное приложение выгодно отличается воспроизводимостью аварийных ситуаций, - установив последователь операций, приводящих к проявлению ошибки, их можно повторить в любое время требуемое количество раз. Это значительно упрощает поиск и устранение источника их возникновения.
Напротив, неправильная синхронизация потоков (как и полное ее отсутствие), порождает трудноуловимые "плавающие" ошибки, проявляющиеся время от времени с некоторой (возможно пренебрежительно малой) вероятностью.
Рассмотрим простейший пример: пусть один поток модифицирует строку, и в тот момент, когда на место завершающего ее нуля помещен новый символ, а завершающий строку ноль еще не добавлен, второй поток пытается скопировать эту строку в свой буфер. Поскольку, завершающего нуля нет, происходит выход за границы массива со всеми вытекающими отсюда последствиями.
Поскольку, потоки в действительности выполняются не одновременно, а вызываются поочередно, получая в своей распоряжение некоторое (как правило, очень большое) количество "тиков" процессора, то вероятность прерывания потока в данном конкретном месте может быть очень мала и даже самое тщательное и широкомасштабное тестирование не всегда способно выловить такие ошибки.
Причем, вследствие трудностей воспроизведения аварийной ситуации, разработчики в подавляющем большинстве случаев не смогут быстро обнаружить и устранить допущенную ошибку, поэтому, пользователям придется довольно длительное время работать с уязвимым приложением, ничем не защищенным от атак злоумышленников.
Печально, что получив в свое распоряжение возможность делить процессы на потоки, многие программисты через чур злоупотребляют этим, применяя потоки даже там, где легко было бы обойтись и без них. Приняв во внимание сложность тестирования многопоточных приложений, стоит ли удивляется крайней нестабильности многих распространенных продуктов?
Не призывая разработчиков отказываться от потоков совсем, автор этой статьи хотел бы заметить, что гораздо лучше распараллеливать решение задач на уровне процессов. Достоинства такого подхода следующие: а) каждый процесс исполняется в собственном адресном пространстве и полностью изолирован от всех остальных; б) межпроцессорный обмен может быть построен по схеме, гарантирующей синхронность и когерентность данных; с) каждый процесс можно отлаживать независимо от остальных, рассматривая его как однопоточное приложения.
К сожалению, заменить потоки уже существующего приложения на процессы достаточно сложно и трудоемко. Но порой это все же гораздо проще, чем искать источник ошибок многопоточного приложения.
Полезные макросы
Вместе с Visual Studio поставляется несколько образцов макросов, которые могут быть использованы не только для изучения Visual Basic'а, но и как самостоятельные утилиты. Нажмите <Shift-Alt-M>, затем в ниспадающем боксе "Macro File" выберите "SAMPLE" и в списке "Macro Name" появится список доступных макросов.
В первую очередь хотелось обратить внимание на макрос "OneTimeInclude", одним мановением руки добавляющий в заголовочный файл программы код, предотвращающий его повторное включение, что, согласитесь, очень удобно:
#ifndef __IDD_xxx_
#define __IDD_xxx_
// Текст программы
#endif //__IDD _xxx_
Весьма полезна и пара макросов "ifdefOut" и "ifndefOut", ограждающих выделенный текст директивами условной компиляции "#ifdef" и "#idndef" соответственно. Условие компиляции запрашивается автоматически в диалоговом окне. Вроде бы мелочь, а как экономит время!
Макрос "ToggleCommentStyle" меняет в выделенном блоке стиль комментариев с '//' на "/* … */" и обратно, что чрезвычайно облегчает приведение всех листингов к единому стилю (особенно это полезно при работе в больших программистских коллективах – свой листинг вы оформляете так, как вам заблагорассудится, а потом просто переформатируете его – и все).
Макрос "PrintAllOpenDocument", как и следует из его названия, просто выводит все открытые активные документы на печать – при работе с большим количеством листингов эта возможность очень удобна.
Макрос "CloseExceptActive" закрывает все активные окна, за исключением текущего, что очень удобно для очистки Студии от "мертвых душ", открытых, но не используемых документов.
Политики записи и продержка когерентности
Если бы ячейки памяти были доступны только на чтение, то их скэшированная копия всегда совпадала бы с оригиналам. Возможность записи (ну какая же программа обходится без операций записи?) рождает следующие проблемы: во-первых, кэш-контроллер должен отслеживать модификацию ячеек кэш-памяти, выгружая в основную память модифицированные ячейки при их замещении, а, во-вторых, необходимо как-то отслеживать обращения всех периферийных устройств (включая остальные микропроцессоры в многопроцессорных системах) к основной памяти. В противном случае, мы рискуем считать совсем не то, что записывали!
Кэш-контроллер обязан обеспечивать когерентность (coherency) – согласованность кэш-памяти с основной памятью. Допустим, к некоторой ячейке памяти, уже модифицированной в кэше, но еще не выгруженной в основную память, обращается периферийное устройство (или другой процессор) – кэш-контроллер должен немедленно обновить основную память, иначе оттуда почитаются "старые" данные. Аналогично, если периферийное устройство (другой процессор) модифицирует основную память, например посредством DMA, кэш-контроллер должен выяснить – загружены ли в модифицированные ячейки в его кэш-память, и если да – обновить их.
Поддержка когерентности – задача серьезная. Самое простое (но не самое лучшее) решение, мгновенно приходящее на ум, – кэшировать ячейки основной памяти только для чтения, а запись осуществлять напрямую, минуя кэш, сразу в основную память. Это, так называемая, сквозная (Write True write policy) политика. Сквозная политика легка в аппаратной реализации, но крайне неэффективна.
Частично компенсировать задержки обращения к памяти помогает буферизация. Записываемые данные на первом этапе попадают не в основную память, а в специальный буфер записи (store/write buffer), размером порядка 32-байт. Там они накапливаются до тех пор, пока буфер целиком не заполниться или не освободиться шина, а затем все содержимое буфера записывается в память "одним скопом". Такой режим сквозной записи с буферизацией (Write Combining write policy) значительно увеличивает производительность системы, но решает далеко не все проблемы.
В частности, значительная часть процессорного времени по-прежнему расходуется именно на выгрузку буфера в основную память. Тем более обидно, что в подавляющем большинстве компьютеров установлен всего один процессор и именно он, а не периферия, интенсивнее всех работает с памятью – не слишком ли дорого обходится поддержка когерентности?
Более сложный (но и совершенный!) алгоритм реализует обратная политика записи (Write Back write policy), до минимума сокращающая количество обращений к памяти. Для отслеживания операций модификации с каждой ячейкой кэш-памяти связывается специальный флаг, называемый флагом состояния. Если кэшируемая ячейка была модифицирована, то кэш-контроллер устанавливает соответствующий ей флаг в грязное (dirty) состояние. Когда периферийное устройство обращается к памяти, кэш-контроллер проверяет – находится ли соответствующий адрес в кэш-памяти и если да, тогда он, глядя на флаг, определяет: грязная она или нет? Грязные ячейки выгружаются в основную память, а их флаг устанавливается в состояние "чисто" (clear). Аналогично – при замещении старых кэш-строк новыми, кэш-контроллер в первую очередь стремится избавиться от чистых кэш-строк, т.к. они могут быть мгновенно удалены из кэша без записи в основную память. И только если все строки грязные – выбирается одна, наименее ценная (с точки зрения политики замещения данных) и "сбрасывается" в основную память, освобождая место для новой, "чистой" строки.
Таким образом, операция записи ячейки занимает от 1 такта процессора до 14-16 тактов системной шины. Такой разнобой объясняется очень просто – если кэш-контроллер поддерживает обратную политику записи, а к записываемой ячейке долгое время никто не обращается и не вытесняет ее из кэша, - кэш-контроллер "сбросит" ее в основную память во время простоя шины, нисколько не отнимая процессорного времени. И всего-то потребуется один такт на запись ячейки в кэш-память. В противном случае (если одно из вышеперечисленных условий не выполняется) расходуется 4-1-1-1 (или 5-1-1-1) тактов системной шины на запись ячейки в основную память и потом еще столько же на загрузку ее в кэш.
Понятие ассоциативности кэша
Проследим по шагам как работает кэш. Вот процессор обращается к ячейке памяти с адресом xyz. Кэш-контроллер, перехватив это обращение, первым делом пытается выяснить: присутствует ли запрошенные данные в кэш-памяти или нет? Вот тут-то и начинается самое интересное! Легко показать, что проверка наличия ячейки в кэш-памяти фактически сводится к поиску
соответствующего диапазона адресов в памяти тегов.
В зависимости от архитектуры кэш-контроллера просмотр всех тегов осуществляется либо параллельно, либо они последовательно перебираются один за другим. Параллельный поиск, конечно, чрезвычайно быстр, но и сложен в реализации (а потому – дорог). Последовательный же просмотр при большом количестве тегов крайне непроизводителен. Кстати, а сколько у нас тегов? Правильно – ровно столько, сколько и кэш-строк. Так, в частности, в 32килобайтном кэше насчитывается немногим более тысячи тегов.
Стоп! Сколько времени потребует просмотр тысячи тегов?! Даже если несколько тегов будут просматриваться за один такт, поиск нужной нам линейки растянется на сотни тактов, что "съест" весь выигрыш в производительности. Нет уж, какая динамическая память ни тормозная, а к ней обратится побыстрее будет, чем сканировать кэш…
Но ведь кэш все таки работает! Спрашивается: как? Оказывается (и это следовало ожидать), что последовательный поиск – не самый продвинутый алгоритм поиска. Существуют и более элегантные решения. Рассмотрим два наиболее популярные из них.
В кэше прямого отображения проблема поиска решается так: пусть каждая ячейка памяти соответствует не любой, а одной строго определенной строке кэша. В свою очередь, каждой строке кэша будет соответствовать не одна, а множество ячеек кэшируемой памяти, но опять-таки, не любых, а строго определенных.
Пусть наш кэш состоит из четырех строк, тогда (см. рис 0х10) первый пакет кэшируемой памяти связан с первой строкой кэша, второй – со второй, третий – с третьей, четвертый – с четвертой, а пятый – вновь с первой! Достаточно очевидно, что адреса ячеек кэшируемой памяти связаны с номерами кэш-строк следующим отношением: , где N – условный номер кэш-линейки, ADDR – адрес ячейки кэшируемой памяти; CACHE.LINE.SIZE – длина кэш-линейки в байтах; CACHE.SIZE – размер кэш-памяти в байтах; "—" – операция целочисленного деления.
Таким образом, чтобы узнать: присутствует ли искомая ячейка в кэш-памяти или нет, достаточно просмотреть всего один-единственный тег соответствующей кэш-линейки, для вычисления номера которого требуется совершить всего три арифметические операции (поскольку, длина кэш-линеек и размер кэш памяти всегда представляют собой степень двойки, операции деления и взятия остатка допускают эффективную и простую аппаратную реализацию). Необходимость просматривать все теги в этой схеме естественным образом отпадает.
Да, отпадает, но возникает другая проблема. Задумайтесь, что произойдет, если процессор попытается последовательно обратиться ко второй, шестой и десятой ячейкам кэшируемой памяти? Правильно – несмотря на то, что в кэше будет полно свободных строк, каждая очередная ячейка будет вытеснять предыдущую, т.к. все они жестко закреплены именно за второй строкой кэша. В результате кэш будет работать максимально неэффективно, полностью вхолостую (trashing).
Программист, заботящийся об оптимизации своих программ, должен организовать структуры данных так, чтобы исключить частое чтение ячеек памяти с адресами, кратными размеру кэша. Понятное дело – такое требование не всегда выполнимо и кэш прямого отображения обеспечивает далеко не лучшую производительность. Поэтому, в настоящее время он практически нигде не встречаются и полностью вытеснен наборно-ассоциативной сверхоперативной памятью.
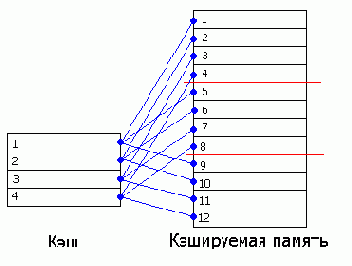
Рисунок 10 0x010 Устройство кэша прямого отображения
Наборно-ассоциативным кэш состоит из нескольких независимых банков,
каждый из которых представляет собой самостоятельный кэш прямого отображения. Взгляните на рисунок 0х012. Видите, каждая ячейка кэшируемой памяти может быть сохранена в любой из двух строк кэш-памяти. Допустим, процессор читает шестую и десятую ячейку кэшируемой памяти. Шестая ячейка идет во вторую строку первого банка, в десятая – во вторую строку следующего банка, т.к. первый уже занят.
Количество банков кэша и называют его ассоциативностью (way).Легко видеть, что с увеличением степени ассоциативности, эффективность кэша существенно возрастает (редкие исключения из этого правила мы рассмотрим позднее в главе "Оптимизация обращения к памяти и кэшу. Влияние размера обрабатываемых данных на производительность").
В идеале, при наивысшей степени дробления, в каждом банке будет только одна линейка, и тогда любая ячейка кэшируемой памяти сможет быть сохранена в любой строке кэша. Такой кэш называют полностью ассоциативным кэшем или просто ассоциативным кэшем.
Ассоциативность кэш-памяти, используемой в современных персональных компьютеров колеблется от двух (2-way cache) до восьми (8-way cache), а чаще всего равна четырем (4-way cache).
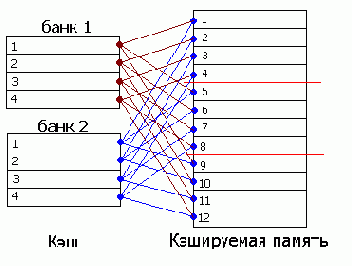
Рисунок 11 0х012 Устройство наборно-ассоциативного кэша
Повтор действий
Для многократного выполнения некоторой операции, скажем, вставки тысячи символов "звездочки", абсолютно незачем кидать кирпичи на клавишу "*" – достаточно воспользоваться командой "SetRepeatCount", устанавливающей количество повторов следующей выполняемой операции. Количество повторов задается либо с цифровой клавиатуры, либо повторными вызовами "SetRepeatCount", при этом количество повторов будет каждый раз умножаться на четыре. Не правда ли здорово?!
Команды "SetRepeatCount0" .. "SetRepeatCount9" изменяют значение счетчика повторов от нуля от девяти соответственно.
Практический сеанс профилировки с VTune в десяти шагах
Любой, даже самый совершенный, инструмент бесполезен, если мастер не умеет держать его в руках. Профилировщик VTune не относится к категории интуитивно-понятных программных продуктов, которые легко осваиваются методом "тыка". VTune – это профессиональный инструмент, и грамотная работа с ним немыслима без специального обучения. В противном случае, большой пласт его функциональных возможностей так и останется незамеченным, заставляя разработчика удивленно пожимать плечами "и что только в этом VTune остальные нашли?".
Настоящая глава ### статья, на учебник не претендует, но автор все же надеется, что она поможет сделать вам в освоении VTune первые шаги и познакомится с его основными функциональными возможностями и к тому же поможет вам решать: стоит ли использовать VTune или же лучше остановить свой выбор на более простом и легком в освоении профилировщике.
В качестве "подопытного кролика" для наших экспериментов с профилировкой и оптимизацией мы используем простой переборщик паролей. Во?первых, это наглядный и вполне реалистичный пример, а, во-вторых, в программах подобного рода требование к производительности превыше всего. Предвидя возможное негодование некоторых читателей, сразу же замечу, что ни о каком взломе настоящих шифров и паролей здесь речь не идет! Реализованный в программе криптоалгоритм не только нигде не используется в реальной жизни, но к тому же допускает эффективную атаку, раскалывающую зашифрованный текст практически мгновенно.
В первую нас очередь будет интересовать не сам взлом, а техника поиска горячих точек и возможные способы их ликвидации. Словом, ничуть не боясь оскорбить свою пуританскую мораль, набейте в редакторе исходный тест следующего содержания:
//----------------------------------------------------------------------------
// Это пример того, как не нужно писать программы! Здесь допущено множество
// ошибок, снижающих производительность. Профилировка позволяет найти их все
// --------------------------------------------------------------------------
// КОНФИГУРАЦИЯ
#define ITER 100000 // макс. итераций
#define MAX_CRYPT_LEN 200 // макс. длина шифротекста
// процедура расшифровки шифротекста найденным паролем
DeCrypt(char *pswd, char *crypteddata)
{
int a;
int p = 0; // указатель текущей позиции расшифровываемых данных
// * * * ОСНОВНОЙ ЦИКЛ РАСШИФРОВКИ * * *
do {
// расшифровываем текущий символ
crypteddata[p] ^= pswd[p % strlen(pswd)];
// переходим к расшифровке следующего символа
} while(++p < strlen(crypteddata));
}
// процедура вычисления контрольной суммы пароля
int CalculateCRC(char *pswd)
{
int a;
int x = -1; // ошибка вычисления CRC
// алгоритм вычисления CRC, конечно, кривой как бумеранг, но ногами чур
// не пинать, - это делалось исключительно для того, чтобы
// подемонстрировать missaling
for (a = 0; a <= strlen(pswd); a++) x += *(int *)((int)pswd + a);
return x;
}
// процедура проверки контрольной суммы пароля
int CheckCRC(char *pswd, int validCRC)
{
if (CalculateCRC(pswd) == validCRC)
return validCRC;
// else
return 0;
}
// процедура обработки текущего пароля
do_pswd(char *crypteddata, char *pswd, int validCRC, int progress)
{
char *buff;
// вывод текущего состояния на терминал
printf("Current pswd : %10s [%d%%]\r",&pswd[0],progress);
// проверка CRC пароля
if (CheckCRC(pswd, validCRC))
{ // <- CRC совпало
// копируем шифроданные во временный буфер
buff = (char *) malloc(strlen(crypteddata));
strcpy(buff, crypteddata);
// расшифровываем
DeCrypt(pswd, buff);
// выводим результат расшифровки на экран
printf("CRC %8X: try to decrypt: \"%s\"\n",
CheckCRC(pswd, validCRC),buff);
}
}
// процедура
перебора паролей
int gen_pswd(char *crypteddata, char *pswd, int max_iter, int validCRC)
{
int a;
int p = 0;
// генерировать
пароли
for(a = 0; a < max_iter; a++)
{
// обработать
текущий пароль
do_pswd(crypteddata, pswd, validCRC, 100*a/max_iter);
// * основной цикл генерации паролей *
// по алгоритму "защелка" или "счетчик"
while((++pswd[p])>'z')
{
pswd[p] = '!';
p++; if (!pswd[p])
{
pswd[p]=' ';
pswd[p+1]=0;
}
} // end while(pswd)
// возвращаем указатель на место
p = 0;
} // end for(a)
return 0;
}
// Функция выводит число, разделяя разряды точками
print_dot(float per)
{
// * * * КОНФИГУРАЦИЯ * * *
#define N 3 // отделять по три разряда
#define DOT_SIZE 1 // размер точки-разделителя
#define DOT "." // разделитель
int a;
char buff[666];
sprintf(buff,"%0.0f", per);
for(a = strlen(buff) - N; a > 0; a -= N)
{
memmove(buff + a + DOT_SIZE, buff + a, 66);
if(buff[a]==' ') break;
else
memcpy(buff + a, DOT, DOT_SIZE);
}
// выводиим на экран
printf("%s\n",buff);
}
main(int argc, char **argv)
{
// переменные
FILE *f; // для чтения исходного файла (если есть)
char *buff; // для чтения данных исходного файла
char *pswd; // текущий тестируемый
пароль (need by gen_pswd)
int validCRC; // для хранения оригинального CRC пароля
unsigned int t; // для замера времени исполнения перебора
int iter = ITER; // макс. кол-во перебираемых паролей
char *crypteddata; // для хранения шифрованных
// build-in default crypt
// кто прочтет, что здесь зашифровано, тот постигнет Великую Тайну
// Крис Касперски ;)
char _DATA_[] = "\x4B\x72\x69\x73\x20\x4B\x61\x73\x70\x65\x72\x73\x6B"\
"\x79\x20\x44\x65\x6D\x6F\x20\x43\x72\x79\x70\x74\x3A"\
"\xB9\x50\xE7\x73\x20\x39\x3D\x30\x4B\x42\x53\x3E\x22"\
"\x27\x32\x53\x56\x49\x3F\x3C\x3D\x2C\x73\x73\x0D\x0A";
// TITLE
printf( "= = = VTune profiling demo = = =\n"\
"==================================\n");
// HELP
if (argc==2)
{
printf("USAGE:\n\tpswd.exe [StartPassword MAX_ITER]\n");
return 0;
}
// выделение
памяти
printf("memory malloc\t\t");
buff = (char *) malloc(MAX_CRYPT_LEN);
if (buff) printf("+OK\n"); else {printf("-ERR\n"); return -1;}
// получение шифротекста для расшифровки
printf("get source from\t\t");
if (f=fopen("crypted.dat","r"))
{
printf("crypted.dat\n");
fgets(buff,MAX_CRYPT_LEN, f);
}
else
{
printf("build-in data\n");
buff=_DATA_;
}
// выделение CRC
validCRC=*(int *)((int) strstr(buff,":")+1);
printf("calculate CRC\t\t%X\n",validCRC);
if (!validCRC)
{
printf("-ERR: CRC is invalid\n");
return -1;
}
// выделение шифрованных данных
crypteddata=strstr(buff,":") + 5;
//printf("cryptodata\t\t%s\n",crypteddata);
// выделение памяти для парольного буфера
printf("memory malloc\t\t");
pswd = (char *) malloc(512*1024); pswd+=62;
/* демонстрация последствий ^^^^^^^^^^^ не выровненных данных */
/* размер блока объясняется тем, что при запросе таких блоков */
/* malloc всегда выравнивает адрес на 64 Кб, что нам и надо */
memset(pswd,0,666); // <-- инициализация
if (pswd) printf("+OK\n"); else {printf("-ERR\n"); return -1;}
// разбор аргументов командной строки
// получение стартового пароля и макс. кол-ва итераций
printf("get arg from\t\t");
if (argc>2)
{
printf("command line\n");
if(atol(argv[2])>0) iter=atol(argv[2]);
strcpy(pswd,argv[1]);
}
else
{
printf("build-in default\n");
strcpy(pswd,"!");
}
printf("start password\t\t%s\nmax iter\t\t%d\n",pswd,iter);
// начало
перебора паролей
printf("==================================\ntry search... wait!\n");
t=clock();
gen_pswd(crypteddata,pswd,iter,validCRC);
t=clock()-t;
// вывод кол-ва перебираемых паролей за сек
printf(" \rPassword per sec:\t");
print_dot(iter/(float)t*CLOCKS_PER_SEC);
return 0;
}
Листинг 11 [Profile/pdsw.c] Не оптимизированный вариант парольного переборщика
Откомпилировав этот пример с максимальной оптимизацией, запустим его на выполнение, чтобы убедиться насколько хорошо справился со своей работой машинный оптимизатор.
Прогон программы на P-III 733 даст скорость перебора… всего лишь порядка 30 тысяч паролей в секунду! Да это меньше, чем совсем ничего и такими темпами зашифрованный текст будет ломаться ну очень долго!!! Куда же уходят такты процессора?
Для поиска узких мест программы мы воспользуемся профилировщиком Intel VTune. Запустим его (не забывая, что под w2k/NT от требует для своей работы привилегий администратора) и, тем временем пока компьютер деловито шуршит винчестером, создадим таблицу символов (не путать с отладочной информацией!), без которой профилировщик ни за что не сможет определить какая часть исполняемого кода к какой функции относится. Для создания таблицы символов в командой строке компоновщика (линкера) достаточно указать ключ "/profile". Например, это может выглядеть так: "link /profile pswd.obj". Если все сделано правильно, образуется файл pswd.map приблизительно следующего содержания:
0001:00000000 _DeCrypt 00401000 f pswd.obj
0001:00000050 _CalculateCRC 00401050 f pswd.obj
0001:00000080 _CheckCRC 00401080 f pswd.obj
Ага, VTune уже готов к работе и терпеливо ждет наших дальнейших указаний, предлагая либо открыть существующий проект – "Open Existing Project" (но у нас нечего пока открывать), либо вызывать Мастера
для создания нового проекта – "New Project Wizard" (вот это, в принципе, нам подходит, но сумеем ли мы разобраться в настойках Мастера?), либо же выполнить быстрый анализ производительности приложения – "Quick Performance Analyses", – выбираем его! В появившемся диалогом окне указываем путь к файлу "pswd.exe" и нажимаем кнопочку "GO" (то есть "Иди").
VTune автоматически запускает профилируемое приложение и начинает собирать информацию о времени его выполнения в каждой точке программы, сопровождая этот процесс симпатичной змейкой - индикатором.
Если нам повезет и мы не зависнем, то через секунду-другую VTune распахнет себя на весь экран и вывалит множество окон с полезной и не очень информацией. Рассмотрим их поближе (см. рис. 0x001). В левой части экрана находится Навигатор Проекта, позволяющий быстро перемещаться между различными его части. Нам он пока не нужен и потому сосредоточим все свое внимание в центр экрана, где расположены окна диаграмм.
Верхнее окно показывает сколько времени выполнялась каждая точка кода, позволяя тем самым обнаружить "горячие" точки (Hot Spots), – т.е. те участки программы, на выполнение которых уходит наибольшее количество времени. В данном случае профилировщик обнаружил 187 горячих точке, о чем и уведомил нас в правой части окна. Обратите внимание на два пика, расположение чуть левее середины центра экрана. Это не просто горячие, а прямо-таки адски раскаленные точечки, съедающие львиную долю быстродействия программы, и именно с их оптимизации и надо начинать!
Подведем курсор к самому высокому пику – VTune тут же сообщит, что оно принадлежит функции out. Постой! Какой out?! Мы ничего такого не вызывали!! Кто же вызвал эту нехорошую функцию? (Несомненно, вы уже догадались, что это сделала функция printf, но давайте притворимся будто бы мы ничего не знаем, ведь в других случаях найти виновника не так просто).
Рисунок 6 0х001 Содержимое окон VTune сразу же после анализа приложения. В первую очередь нас интересует верхнее окно, "картографирующее" горячие точки, расположенные согласно их адресам. Нижнее окно содержит информацию о относительном времени выполнении всех модулей системы. Обратите внимание, модуль pswd.exe (на диаграмме он отмечен стрелкой) занял далеко не первое место и основную долю производительности "съел" кто-то другой. Создается обманчивое впечатление, что оптимизировать модуль pswd.exe бессмысленно, но это не так…
Чтобы не рыскать бес толку по всему коду, воспользуется другим инструментом профилировщика – "Call Graph", позволяющим в удобной для человека форме отобразить на экране иерархическую взаимосвязь различных функций (или классов – если вы пишите на Си ++).
В меню "Run" выбираем пункт "Win32* Call Graph Profiling Session" и вновь идем перекурить, пока VTune профилирует приложение. По завершению профилировки на экране появится еще два окна. Верхнее, содержащее электронную таблицу, мы рассматривать не будем (оно понятно и без слов), а вот к нижнему присмотримся повнимательнее. Пастельно-желтый фон украшают всего два ядовито-красных прямоугольника с надписями "Thread 400" и "mainCRTStartup". Щелкнем по последнему из них два раза, – VTune тут же выбросит целый веер дочерних функций, вызываемых стартовым кодом приложения. Находим среди них main (что будет очень просто, т.к. только main выделен красным цветом) и щелкаем по нему еще раз…. и будем действовать так до тех пор, пока не раскроем все дочерние функции процедуры main.
В результате выяснится, что функцию out действительно вызывает функция printf, а саму printf вызывает… do_pswd. Ну, да! Теперь мы "вспомнили", что использовали ее для вывода текущего тестируемого пароля на экран! Какая глупая идея! Вот оказывается куда ушла вся производительность!

Рисунок 7 0х002 Иерархия "горячих" функций, построенная Мастером Call Graph. Цвет символизирует "температуру" функции, а стоящее возле нее число сообщает сколько именно она вызвалась раз.
Практическое использование предвыборки
Если вычислительный алгоритм позволяет с той или иной вероятностью предсказать адрес следующей обрабатываемой ячейки – это хороший кандидат на оптимизацию, причем выигрыш от использования предвыборки будет тем значительнее, чем точнее определяется адрес следующей обрабатываемой ячейки. В первую очередь это относится к циклам с постоянным шагом, геометрическим преобразованиям в 2D/3D графике, операциям сортировки, копирования и инициализация памяти, строковым операциям и т.д. В меньшей степени поддается оптимизации обработка списков и двоичных деревьев. Поскольку, порядок размещения их элементов заранее не известен и определяется исключительно в процессе прохода по списку (дереву), гарантированно определить адрес следующего обрабатываемого элемента в общем случае невозможно. Однако достаточно часто его удается угадать. Например, можно предположить, что начало очередного элемента находится непосредственно за концом текущего. Если список (двоичное дерево) не очень сильно фрагментирован, процент попаданий значительно превосходит количество промахов и предвыборка дает положительный эффект.
Рассмотрим следующий пример:
#define STEP_SIZE L1_CACHE_LINE_SIZE
for(a=0;a<BLOCK_SIZE;a+=STEP_SIZE)
{
// Делаем некоторые вычисления (какие - не важно)
_jn(c, b);
// Считываем очередную ячейку
b+=p[c];
}
Листинг 20 Кандидат на оптимизацию с использованием предвыборки
Если обрабатываемый блок отсутствует в кэше первого и второго уровней, а шаг цикла равен или превышает размер кэш-линейки, то каждое обращение к памяти будет вызывать значительную задержку – порядка 10-12 тактов системной шины, требующихся на передачу запрашиваемых ячеек из медленной оперативной памяти в быстрый кэш. На P-III 733 это составит более полусотни тактов процессора! В результате – время выполнения данного примера в большей степени зависит от быстродействия подсистемы памяти, и в меньшей – от тактовой частоты процессора.
Однако поскольку адрес очередной обрабатываемой ячейки известен заранее, данные можно загружать в кэш параллельно с выполнением вычислений.
Пример, оптимизированный под P-III, в первом приближении будет выглядеть приблизительно так:
#define STEP_SIZE L1_CACHE_LINE_SIZE
for(a=0;a<BLOCK_SIZE;a+=STEP_SIZE)
{
// Даем команду на загрузку следующей 32-байтной строки
// в L1-кэш. Загрузка будет осуществляться параллельно
// с выполнением функции _jn.
// Когда же соответствующая ячейка будет затребована,
// она уже окажется в L1-кэше, откуда процессор сможет
// извлечь ее безо всяких задержек.
_prefetchnta(p+c+STEP_SIZE);
// ^^^^^^^^ обратите внимание: в кэш
// загружается ячейка, обрабатываемая не в текущей, а
// следующей итерации цикла. Дело в том, что за время
// выполнения функций _jn запрашиваемая кэш-линейка
// просто не успевает загрузится!
// (подробнее см. "Планирование дистанции предвыборки")
// Выполняем некоторые вычисления
_jn(c, b);
// Считываем очередную ячейку
// Во всех, кроме первой, итерациях цикла ячейка будет
// гарантированно находиться в кэше первого уровня,
// в результате время ее чтения сократится до 1 такта CPU
b+=p[c];
}
Листинг 21 Оптимизированный вариант с использованием предвыборки [P-III]
На P-III 733/133/100 оптимизированный вариант выполняется быстрее на целых 64%, а на AMD Athlon 1050/100/100 – на ~60%, т.е. предвыборка увеличивает производительность более чем в два раза! (см. рис. 0х014) И это притом, что в цикле выполняется лишь одно обращение к памяти за каждую итерацию. А чем больше происходит обращений к памяти – тем больший выигрыш дает оптимизация!
Максимальный прирост производительности достигается в тех случаях когда: а) предвыборка данных осуществляется в кэш иерархию, соответствующую их назначению; б) запрашиваемые данные загружаются аккурат к моменту обращения; в) осуществляется предвыборка только тех данных, которым она действительно требуется (хотя prefetchx
– не блокируемая инструкция, и достаточно интеллектуальная для того, чтобы не загружать данные, уже находящиеся в кэше, ее обработка достается "не бесплатно" и лишние вызовы снижают производительность).
На P-4 данный пример в оптимизации вообще не нуждается, – процессор и сам, определив последовательность обращений к данным, осуществит их упреждающую загрузку самостоятельно. Инструкция программной предвыборки будет лишним балластом, лишь снижающим производительность системы (впрочем, не намного).
Для переноса примера 21 на K6 (VIA C3) достаточно лишь заменить инструкцию prefetchnta
на ее ближайший аналог – prefetch. А вот с переносом на Athlon дела обстоят намного сложнее. Попав на него, приведенный выше пример оптимизации покажет далеко не лучший результат: во-первых, предвыборка данных просто не успеет осуществиться за время выполнения функции _jn (ведь Athlon намного быстрее K6!) и процессор будет вынужден какое-то время простаивать, ожидая заполнения 64-байтной линейки кэша второго уровня. Во-вторых, вследствие того, что кэш-линейки на Athlon вдвое длиннее, чем на K6 (VIA C3), каждый второй запрос на предвыборку становятся бесполезным балластом, впустую отъедающим процессорное время. Проблема, однако!
Но программисты – на то они и программисты, чтобы не искать легких путей. К тому же, все проблемы решаемы…
Рисунок 39 graph 0x014 Эффективность программной предвыборки в оптимизации примера 21
Правило I
Прежде, чем оптимизировать код, обязательно следует иметь надежно работающий не оптимизированный вариант или "...put all your eggs in one basket, after making sure that you've built a really *good* basket" ("…прежде, чем класть все яйца [не обязательно именно свои яйца – прим. КК] в одну корзину – убедись, что ты построил действительно хорошую корзину). Т.е. прежде, чем приступать к оптимизации программы, убедись, что программа вообще-то работает.
Создание оптимизированного кода "на ходу", по мере написания программы, невозможно! Такова уж специфика планирования команд – внесение даже малейших изменений в алгоритм практически всегда оборачивается кардинальными переделками кода. Потому, приступайте к оптимизации только после тренировки на "кошках", – языке высокого уровня. Это поможет пояснить все неясности и темные места алгоритма. К тому же, при появлении ошибок в программе подозрение всегда падает именно на оптимизированные участки кода (оптимизированный код за редкими исключениями крайне ненагляден и чрезвычайно трудно читаем, потому его отладка – дело непростое), – вот тут-то и спасает "отлаженная кошка". Если после замены оптимизированного кода на не оптимизированный ошибки исчезнут, значит, и в самом деле виноват оптимизированный код. Ну, а нет, – ищите их где-нибудь в другом месте.
Правило II
Помните, что основой прирост оптимизации дает не учет особенностей системы, а алгоритмическая оптимизация.
Никакая, даже самая "ручная" оптимизация не позволит существенно увеличить эффективность пузырьковой сортировки или процедуры линейного поиска. Правильное планирование команд и прочите программистские трюки ускорят программу в лучшем случае в несколько раз. Переход к быстрой сортировке (quick sort) и двоичному поиску сократят время обработки данных как минимум на порядок, – как бы криво ни был написан программный код. Поэтому, если ваша программа выполняется слишком медленно, лучше поищите более эффективные математические алгоритмы, а не выжимайте из изначально плохого алгоритма скорость по капле.
Правило III
Не путайте оптимизацию кода и ассемблерную реализацию.
Обнаружив профилировщиком узкие места в программе, не торопитесь переписывать их на ассемблер. Сначала убедитесь, что все возможное для увеличения быстродействия кода в рамках языка высокого уровня уже сделано. В частности, следует избавиться от прожорливых арифметических операций (особенно обращая внимание на целочисленное деление и взятие остатка), свести к минимуму ветвления, развернуть циклы с малым количеством итераций… в крайнем случае, попробуйте сменить компилятор (как было показано выше – качество компиляторов очень разниться друг к другу). Если же все равно останетесь недовольны результатом тогда…
Правило IV
Прежде, чем порываться переписывать программу на ассемблер, изучите ассемблерный листинг компилятора на предмет оценки его совершенства.
Возможно, в неудовлетворительной производительности кода виноват не компилятор, а непосредственно сам процессор или подсистема памяти, например. Особенно это касается наукоемких приложений, жадных до математических расчетов и графических пакетов, нуждающихся в больших объемах памяти. Наивно думать, что перенос программы на ассемблер увеличит пропускную способность памяти или, скажем, заставит процессор вычислять синус угла быстрее. Получив ассемблерный листинг откомпилированной программы (для Microsoft Visual C++, например, это осуществляется ключом "/FA"), бегло просмотрите его глазами на предмет поиска явных ляпов и откровенно глупых конструкций наподобие: "MOV EAX,[EBX]\MOV [EBX],EAX". Обычно гораздо проще не писать ассемблерную реализацию с чистого листа, а вычищать уже сгенерированный компилятором код. Это требует гораздо меньше времени, а результат дает ничуть не худший.
Правило V
Если ассемблерный листинг, выданный компилятором, идеален, но программа без видимых причин все равно исполняется медленно, не отчаивайтесь, а загрузите ее в дизассемблер. Как уже отмечалось выше, оптимизаторы крайне неаккуратно подходят к выравниванию переходов и кладут их куда глюк на душу положит. Наибольшая производительность достигается при выравнивании переходов по адресам, кратным шестнадцати, и будет уж совсем хорошо, если все тело цикла целиком поместиться в одну кэш-линейку (т.е. 32 байта). Впрочем, мы отвлеклись. Техника оптимизации машинного кода – тема совершенно другого разговора. Обратитесь к документации, распространяемой производителями процессоров – Intel и AMD.
Правило VI
Если существующие команды процессора позволяют реализовать ваш алгоритм проще и эффективнее, – вот тогда действительно, тяпнув для храбрости пивка, забросьте компилятор на полку и приступайте к ассемблерной реализации с чистого листа. Однако с такой ситуацией приходится встречаться крайне редко, и к тому же не стоит забывать, что вы – не на одиноком острове. Вокруг вас – огромное количество высокопроизводительных, тщательно отлаженных и великолепно оптимизированных библиотек. Так зачем же изобретать велосипед, если можно купить готовый?
Правило VII
Если уж взялись писать на ассемблере, пишите максимально "красиво" и без излишнего трюкачества. Да, недокументированные возможности, нетрадиционные стили программирования, "черная магия", – все это безумно интересно и увлекательно, но… плохо переносимо, непонятно окружающим (в том числе и себе самому после возращения к исходнику десятилетней давности) и вообще несет в себе массу проблем. Автор этих строк неоднократно обжигался на своих же собственных трюках, причем самое обидное, что трюки эти были вызваны отнюдь не "производственной необходимостью", а… ну, скажем так, "любовью к искусству". За любовь же, как известно, всегда приходится платить. Не повторяете чужих ошибок! Не брезгуйте комментариями и непременно помещайте все ассемблерные функции в отдельный модуль. Никаких ассемблерных вставок – они практически непереносимы и создают очень много проблем при портировании приложений на другие платформы или даже при переходе на другой компилятор.
Единственная предметная область, не только оправдывающая, но, прямо скажем, провоцирующая ассемблерные извращения, это – защита программ, но это уже тема совсем другого разговора…
и VIA C3 программная предвыборка
В K6\Athlon и VIA C3 программная предвыборка осуществляется одной из двух инструкций prefetch
или prefetchw. Суффикс на конце последней сообщает процессору, что загружаемые данные планируется модифицировать. Это отнюдь не означает, что данные, загружаемые, посредством prefetch, модифицировать нельзя. Модифицировать их можно, но не желательно, т.к. в этом случае процессор вынужден совершать дополнительный цикл, изменяя атрибуты соответствующей кэш-линейки с эксклюзивной
на модифицируемую.
Эксклюзивные, т.е. неизменяемые кэш-линейки, при их вытеснении их кэша просто выбрасываются в битовую корзину, иначе называемую устройством /dev/null или "черной дырой".
Модифицируемые же кэш-строки независимо от того, были ли они реально модифицированы или нет, всегда вытесняются в оперативную память (кэш вышестоящего уровня), что требует определенного количества тактов процессора (подробнее см. "Кэш –Принципы функционирования. Организация кэша. Протокол MESI").
Инструкция prefetch
просто инициирует запрос ячейки памяти, точно так, как это делает любая команда, обращающаяся к памяти, но, в отличие от последней, prefetch
не помещает загружаемые данные ни в какой регистр, более того, она вообще не дожидается окончания загрузки этих данных, тут же возвращая управление. Преждевременное завершение инициатора запроса еще не освобождает кэш-контроллер от обязанности выполнения этого запроса, но, если запрошенная ячейка уже находится в кэше первого уровня, – ничего не происходит и инструкция prefetch
ведет себя аналогично команде NOP (нет операции). В противном случае кэш-контроллер обращается к кэшу второго уровня, а если искомой ячейки не оказывается и там – к оперативной памяти (кэшу третьего уровня), целиком заполняя соответствующие кэш-строки кэшей всех нижестоящих уровней. (Длина кэш-строк составляет 32 байта на AMD K6 (VIA C3) и 64 байта на Athlon\Duron). Поскольку кэш-контроллер работает независимо от вычислительного конвейера процессора, предвыборка позволяет загружать очередную порцию данных параллельно с обработкой предыдущей.
Если время загрузки данных не превышает времени их обработки, то простоя процессора вообще не происходит – вычислительный конвейер вращается безостановочно, а время доступа к памяти полностью маскируется.
Инструкция prefetchw
работает аналогично prefetch, но автоматически присваивает загружаемой строке статус модифицируемой. Если строку действительно планируется модифицировать, это сэкономит от 15 до 25 тактов процессорного времени. Обратно, если вы неуверенны – будет ли реально модифицировать строка или нет, лучше загрузите ее как исключительную, т.к. выгрузка модифицируемой, но реально не модифицированной строки в оперативную память обойдется намного дороже.
Несмотря на то, что AMD позиционирует команды предвыборки как аппаратно-независимые, они таковыми не являются, поскольку, количество байт, загружаемых инструкциями prefetch
и prefetchw,
определяется размером кэш-линий процессора, а их длина различна: 32 байта для K-6 (VIA C3) и 64 байта для Athlon\Duron. Соответственно, различны оптимальный шаг и минимальная дистанция предвыборки (подробнее см. "Практическое использование предвыборки/Планирование дистанции предвыборки").
В этом свете становится очень интересным следующее высказывание AMD, почерпнутое из руководства по оптимизации под Athlon: "The PREFETCHNTA/T0/T1/T2 instructions in the MMX extensions are processor implementation dependent. If the developer needs to maintain compatibility with the 25 million AMD-K6 ® - 2 and AMD-K6-III processors already sold, use the 3DNow! PREFETCH/W instructions instead of the various prefetch instructions that are new MMX extensions", что в переводе на русский звучит приблизительно так: "Инструкции PREFETCHNTA/T0/T1/T2 из MMX-расширения аппаратно зависимы. Если вы, господин разработчик, нуждаетесь в совместимости с 25 миллионами уже проданных процессоров AMD-K6®-2 и AMD-K6-III, вместо инструкций предвыборки нового расширения MMX, пользуйтесь командами PREFETCH/W из расширения 3DNow!"
Вот вам хорошая демонстрация искусства умолчания! Если уж бросать камень в огород Intel, то нелишне бы отметить, что, во-первых, и собственные инструкции предвыборки аппаратно зависимы, а, во-вторых, процессорами Pentium они не поддерживается. Так что никаких преимуществ у AMD'ушной предвыборки перед Intel нет и использовать ее не рекомендуется.
программная предвыборка осуществляется следующими
В процессорах P-III и P- 4 программная предвыборка осуществляется следующими инструкциями: prefetchnta, prefetcht0, prefetcht1, prefetcht2. Суффикс указывает на тип загружаемых данных, что определяет уровень кэш-иерархии, в которую эти данные будут загружены. Так, "NTA" расшифровывается как "Non-TemporAl [Data]" – не временные данные, т.е. данные, многократное использование которых не планируется. Соответственно "T0", "T1" и "T2" обозначает временные данные, использовать которые планируется неоднократно.
Какой бы командной предвыборка ни осуществлялась, кэш - линейкам, загружаемым из основной памяти, всегда присваивается эксклюзивный
статус. При предвыборке линеек из кэша второго уровня, их прежний статус сохраняется. Возможность загрузки кэш-линейки с автоматической установкой статуса модифицируемой в процессорах Pentium не реализована. Однако ввиду многоступенчатой схемы буферизации записи, изменение атрибутов кэш-линеек происходит в основном, а не дополнительном, как в K6\Athlon, цикле обмена, т.е. без ущерба для производительности.
Причем, в отличие от prefetch/w, инструкции prefetchnta/t0/t1/t2 не приказывают, а рекомендуют (или, если так угодно, – просят) осуществить предвыборку. Процессор отклоняет просьбу и не осуществляет предвыборку, если:
· запрошенные данные уже содержится в кэше соответствующей или ближайшей к процессору иерархии;
· сведения о станице, к которой принадлежат загружаемые данные, отсутствуют в DTLB (Data Translation Look aside Buffer – Буфере Ассоциативной Трансляции);
· подсистема памяти процессора занята перемещением данных между L1- и L2-кэшем;
· запрошенные данные принадлежат региону некэшируемой памяти (странице с атрибутами UC или USWC);
· данные не могут быть загружены из-за ошибки доступа (при этом исключение не вырабатывается);
· инструкция предвыборки предваряется префиксом LOCK (в этом случае генерируется исключение "неверный опкод").
Во всех остальных случаях предвыборка выполняется. Алгоритм ее выполнения аппаратно - зависим и сильно варьируется от одной модели процессора к другой, поэтому, поведение "предвыборных" команд на P-III и P-4 ниже рассматривается по отдельности.
Pentium-III:
Инструкция prefetchnta
загружает данные в кэш первого уровня, минуя кэш-второго. Действительно, данные, повторное обращение к которым не планируется, целесообразно помещать в кэш самой ближайший к процессору иерархии, не затирая содержимое остальных, т.к. оно может еще пригодиться, а вот однократно используемые данные после их вытеснения из L1-кэша, из L2-кэша затребованы уж точно не будут.
Инструкция prefetcht0
загружает данные в кэш иерархии обоих уровней. Данные, обращение к которым происходит многократно, будучи загруженными в L2-кэш, окажутся как нельзя кстати, когда будут вытеснены из L1-кэша.
Инструкции prefetcht1 и prefetcht2
загружают данные в один лишь кэш второго уровня, не помещая их в кэш первого. Поскольку, выгрузка буферов записи происходит в кэш второго уровня, минуя первый, то предвыборку соответствующих линеек в L1-кэш осуществлять нецелесообразно. Вот тут-то и пригодится prefetcht1/t2!
Размер загружаемых данных равен длине кэш-линеек соответствующей иерархии и составляет 32 байта.
Pentium-4:
Ни одна из команд предвыборки P-4 не позволяет загружать данные в кэш первого уровня. Все – и временные, и не временные данные помещаются лишь в кэш второго уровня, поскольку… поскольку, создатели процессора захотели поступить именно так. Эффективность такой стратегии дискуссионна, но, как бы там ни было, время доступа к кэшу второго уровня, намного меньше времени доступа к оперативной памяти, поэтому, даже такая предвыборка все же значительно лучше, чем ничего.
Возникает вопрос – если все команды предвыборки помещают загружаемые данные в кэш второго уровня, то какая между ними разница? Между командами prefetcht0, prefetcht1 и prefetcht2 – действительно, никакой.
А вот команда prefetchnta
отличается тем, что помещает загружаемые данные не в любой, а исключительно в первый банк кэша второго уровня (восьми ассоциативный L2-кэш P-4 содержит восемь таких банков), благодаря чему prefetchnta
никогда не вытесняет более 1/8 объема кэша второго уровня. Однократно используемые данные, как уже говорилось выше, действительно, не должны вытеснять многократно используемые данные из верхних кэш-иерархий, но в P-4 такое вытеснение все же происходит, и предотвратить его, увы, нельзя. Причем, вытесняются отнюдь не те ячейки, к которым дольше всего не было обращений, а линейки фиксированного банка, возможно интенсивно используемые обрабатываемым их приложением! Словом, в P-4 программная предвыборка реализована далеко не лучшим образом – непродуманно, что называется "спустя рукава". (Не иначе как дикая конкурентная спешка дает о себе знать).
Размер загружаемых данных равен длине линеек кэша второго уровня, что составляет 128 байт.
Различия в реализации предвыборки на P-III и P-4 существенно затрудняют оптимизацию приложений, поскольку каждый процессор требует к себе особого, индивидуального подхода и одновременно угодить всем им невозможно. Для достижения максимальной эффективности все критические процедуры рекомендуется реализовывать как минимум в двух вариантах – отдельно для P-III и отдельно для P-4. В противном случае, либо P?III будет зверски тормозить, либо P-4 не раскроет подлинного потенциала своей производительности. Учитывая существование K6\Athlon процессоров, вариантов реализации набирается уже четыре. Не слишком ли много головной боли для программистов? Нет, это вовсе не призыв к отказу от предвыборки, – в ряде случаев такой отказ просто невозможен. Это всего лишь незлобное ворчание замученного программиста… (А программисты, как и комсомольцы, легкими путями не избалованы).
Препроцессор
Каждый, кто работал с листингами (особенно чужими), знает: какую сумятицу вносят директивы условной компиляции. Допустим, встречается в тексте директива "#ifdef _A_". Как определить – какие строки программы относятся к ее телу, а какие нет? Теоретически в этом нет ничего сложного – достаточно найти директиву "#else" или "#endif", но как ее найти? Контекстный поиск здесь непригоден. Поскольку директивы условной компиляции могут быть вложенными, нет никаких гарантий, что ближайший найденный "#endif" или "#else" относится к той же самой директиве "#ifdef". Приходится пролистывать программу вручную, мысленно отслеживая все вложения и переходы. Однако это, во-первых, очень медленно, а во-вторых, так легко "прозевать" несколько директив, особенно если они разделены большим количеством строк.
К счастью, Visual Studio умеет трассировать директивы условной компиляции в обоих направлениях. Правда, по совершенно непонятым мотивам эта возможность не афишируется и вообще скрыта от посторонних глаз.
Если курсор находится в теле одной из ветвей директивы условной компиляции (т.е. либо ветви "#if … #else", либо "#else … #endif", либо "#if … #endif"), то нажатием <Ctrl-K> мы переместимся в ее конец! Повторное нажатие приведет к переходу либо на следующую ветвь, либо (если текущая ветвь исчерпана) – на следующую вышележащую директиву. Во избежание путаницы обращайте внимание на строку статуса: переход с ветви на ветвь сопровождается сообщением: "Matching #ifdef..#endif found", а переход к вложенной директиве – "Enclosing #ifdef..#endif found". Соответственно, сообщение "No Enclosing #ifdef..#endif found" говорит о том, что ничего найти не удалось.
Для обратной трассировки (т.е. прохождению цепочки директив снизу вверх) нажмите <Ctrl-J>.
Комбинации <Shift-Ctrl-K> и <Shift-Ctrl-J> автоматически выделяют тело трассируемых директив, – это очень полезно, если его планируется копировать в буфер или вообще вырезать из программы.
Трассировка условных директив – это просто сказка, в которую беззаветно влюбляешься с первых же минут знакомства! Изучение SDK'шных файлов, таких, например, как WINNT.H без нее просто немыслимо!
#ifdef
_A_ // ß
если здесь нажать Ctrl-K, мы переместимся в L1
// много строк текста
#ifdef
_B_
// много строк текста
#else // ß
если здесь нажать Ctrl-K, мы переместимcя в S1
// много строк текста
#endif // à
S1
#else // à
L1
// много строк текста
#endif
Причины и последствия ошибок переполнения
В большинстве языков программирования, в том числе и в Cи/Cи++, массив одновременно является и совокупностью определенного количества данных некоторого типа, и безразмерным
регионом памяти. Программист может получить указатель на начало массива, но не имеет возможности непосредственно определить его длину. Си/Cи ++ не делает особых различный между указателями на массив и указателями на ячейку памяти, и позволяет выполнять с указателями различные математические операции.
Мало того, что контроль выхода указателя за границы массива всецело лежит на плечах разработчика, строго говоря, этот контроль вообще невозможен в принципе! Получив указатель на буфер, функция не может самостоятельно вычислить его размер и вынуждена либо полгать, что вызывающий код выделил буфер заведомо достаточно размера, либо требовать явного указания длины буфера в дополнительном аргументе (в частности, по первому сценарию работает gets, а по второму – fgets).
Ни то, ни другое не может считаться достаточно надежным, - знать наперед сколько памяти потребуется вызывающей функции (за редкими исключениями) невозможно, а постоянная "ручная" передача длины массива не только утомительна и непрактична, но и ничем не застрахована от ошибок (можно передать не тот размер или размер не того массива).
Другая частая причина возникновения ошибок переполнения буфера: слишком вольное обращение с указателями. Например, для перекодировки текста может использоваться такой алгоритм: код преобразуемого символа складывается с указателем на начало таблицы перекодировки и из полученной ячейки извлекается искомый результат. Несмотря на изящество этого (и подобных ему алгоритмов) он требует тщательного контроля исходных данных – передаваемый функции аргумент должен быть неотрицательным числом не превышающим последний индекс таблицы перекодировки. В противном случае произойдет доступ совсем к другим данным. Но о подобных проверках программисты нередко забывают или реализуют их неправильно.
Можно выделить два типа ошибок переполнения: одни приводят к чтению не принадлежащих к массиву ячеек памяти, другие – к их модификации.
В зависимости от расположения буфера за его концом могут находится: а) другие переменные и буфера; б) служебные данные (например, сохраненные значения регистров и адрес возврата из функции); с) исполняемый код; д) никем не занятая или несуществующая область памяти.
Несанкционированное чтение не принадлежащих к массиву данных может привести к утере конфиденциальности, а их модификация в лучшем случае заканчивается некорректной работой приложения (чаще всего "зависанием"), а худшем – выполнением действий, никак не предусмотренных разработчиком (например, отключением защиты).
Еще опаснее, если непосредственно за концом массива следуют адрес возврата из функции – в этом случае уязвимое приложение потенциально способно выполнить от своего имени любой код, переданный ему злоумышленником! И, если это приложение исполняется с наивысшими привилегиями (что типично для сетевых служб), взломщик сможет как угодно манипулировать системой, вплоть до ее полного уничтожения!
Сказанное справедливо и для случая, когда вслед за буфером, подверженном переполнению, расположен исполняемый код. Однако, в современных операционных системах такая ситуация практически не встречается, поскольку они довольно далеко разносят код, данные и стек друг от друга.
А вот наличие несуществующей станицы памяти за концом переполняющегося буфера – не редкость. При обращении к ней процессор генерирует исключение в большинстве случаев приводящее к аварийному завершению приложения, что может служить эффективной атакой "отказа в обслуживании".
Таким образом, независимо от того где располагается переполняющийся буфер – в стеке, сегменте данных или в области динамической памяти (куче), он делает работу приложения небезопасной.
Поэтому, представляет интерес поговорить о том, можно ли предотвратить такую угрозу и если да, то как.
Придя в этот мир - оглянись!
- Если ты убедишь себя, искренно сможешь нести любую галиматью (что за очаровательное старинное слово; проверь, что оно значит), совершеннейший бред в каждом слове и тебе поверят. Но только не один из наших ясновидцев.
Френк Херберт "Дом Глав Дюны"
Все – и старый подсвечник, и таинственный заговор полумрака в колеблющемся пламени свечи, казалось нереальным в тусклом свете нагроможденных мониторов и повсюду змеящихся проводов. Но у Криса были свои странности. Огонь нес в себе какую-то долю мистицизма, ушедшего в песок истории. Цивилизация достигла своих высот здесь, в конце 20 столетия. И пик взлета грозил обернуться распадом и деградацией. Устойчивость зиждилась лишь на тонком волоске безразличия. Все были слишком заняты, что бы остановиться и обернуться вокруг. Посмотреть на небо, на капельки росы, стекающие с листка, вздохнуть полной грудью, и удобно усевшись в кресле потянуться за кремнием, что бы зажечь свечу.
Электрический свет сделал все таким простым, и очевидным, что не осталось вопросов, которые было бы можно задать. Но как неузнаваемо может измениться та же обстановка, если зажечь Свечу. Таинственный полумрак – это Пустыня истории. Ветер Пустыни колеблет Свечу, и обдает Путника обжигающем дыханием пустыни. Ноги вязнут в песке, каждый шаг – это преодоление собственной беспомощности перед природой. Еще одна сложность, но идти надо. Движение – это жизнь. В этой стихии песка и ветра ты один на тысячи миль вокруг. Никто не сможет помочь в борьбе с природой. Если ты проиграешь, она поглотит тебя, даже не заметив этого. Если ты выживешь, она все равно этого не заметит. Кто же ты, Путник - мыслящий человек или песчинка в Пустыне?
Человек победил Пустыню, проложив железные дороги, построив самолеты, но не смог в этом убедить себя. Можно скрыться в шумном и многолюдном Городе, куда не достает ветер и не проникает песок. Но в этом нагромождении пластика и бетона становишься песчинкой социума. Город тебя подминает, но никто не замечает этого. Бежать уже некуда.
Открыт лишь один путь – назад в Пустыню, где ты будешь один на один в борьбе за существование.
Как и у всего на свете, у одиночества есть свои плюсы и минусы. Ты работаешь один, без подстраховки, и если оступишься – смерть. Но никто не ограничивает в выборе путей достижения цели. Ты ОДИН. Ты верховный судья, Бог и Дьявол в одном теле. Границ нет, все пространство вокруг открыто. Иди куда хочешь. Иди, но если ошибешься в направлении – уйдешь в пески Пустыни без воды и еды. Ветер заметет твои следы и никто не найдет где кончился твой путь...
И сколько бы не светило Солнце, а люди всегда шли. Кто-то бежал, подальше от Города, преследуемый законом, кто-то возненавидел ближних своих, ну а кто-то уходил в Пустыню от одиночества. Там оно не было таким гнетущим, как вокруг не замечающих тебя людей.
В Пустыне все они равны... изгнанники Города, не важно, по какой причине. Все сталкиваются с одними и теми же проблемами солнца, еды и воды. Неверно думать, что ни того, ни другого нет в раскаленном песке, обжигающем ноги. Даже в Центре, где воздух сухой и колючий, все же можно найти немного влаги. Ночью, когда воздух достаточно охладиться, она конденсируется в капельки росы – стоит только положить на песок холодный предмет. Правда, к утру влага испаряется, так что надо спешить.
Ночи в Пустыне – вообще удивительное явление. Небо темнеет быстро и, словно остывая вместе с Пустыней, плавно меняет цвет, еще долго оставаясь раскаленным оранжевым маревом у западной кромки горизонта. Изнуряющая жара внезапно сменяется бьющей ознобом прохладой. В Пустыне нет дров, чтобы развести костер, а сухие колючки сгорают быстро и совсем не дают углей. Однако огонь может привлечь внимание мелких ящерок и других пресмыкающихся, мясо придает вам сил.
В этой борьбе грань между человеком и животным очень тонка. Природа берет свое, и первобытные инстинкты начинают доминировать над разумом. Это очень скользкая игра в прятки с самим собой. Прошлые сознания всплывает из памяти и подминает тебя настоящего...
Крис размышлял: кем он был в настоящий момент. Мимолетное изменение восприятия не сулило ничего хорошего. Нервы были и без того слишком напряжены. Еще один подарок судьбы – это уж слишком… Слишком многое произошло за последний месяц… Его стихия сократилась до предела, сжалась в маленькую скорлупу и все существо звало убежать, спрятаться, затаиться и переждать нашедшие на Город свинцовые тучи.
Крис еще не знал, что в этой борьбе у него окажется союзник. Привыкший к одиночеству, он всегда полагался лишь на самого себя, на собственные силы, навыки и умения, даже когда их явно не хватало. До этого ему элементарно везло. Стоило лишь сделать шаг назад, как он оказывался далеко впереди. Необъяснимо с точки зрения здравого смысла, но факт. А может быть, так лишь казалось. В Пустыне нет ориентиров. "взад" и "вперед" – слишком субъективные ощущения, чтобы быть до конца в них уверенным.
Но чем больше везет, тем больше боишься проиграть. Неуверенность в себе притупляет интуицию и начинаешь действовать нервно, хаотично, наугад, только усугубляя положение.
Чтобы ничего не бояться, приходилось ничего не иметь. Не привязываться к вещам, не обрастать мебелью, не привязываться к людям. Жить кочевой жизнью, переезжая из квартиры в квартиру, где только голые стены, диван да компьютер.
В какой-то степени это даже нравилось. Просто было интересно, бродить по новым местам, осваивать новые территории... находить себе новые сложности, с удовлетворением отмечая, что каждый раз их решать все легче и легче, а вот находить становилось труднее...
* * *
Пустыня не делит путников на женщин и мужчин, но так уж получилось, что мужчин было всегда больше. Женщины существа на удивление домашние, привязанные к семейному очагу. Может быть поэтому, Крис никогда не задумывался, что он может Там ее встретить. С чем можно было говорить с девушкой из Города, если она не видела ни неба, ни звезд, ни этих бескрайних песчаных просторов, ни стояла на гребнях дюн, рискуя сорваться, оказавшись погребенной под тоннами песка.
В Городе нет пространств, и нет горизонта. В этой тесноте редко кто ухитряются видеть дальше собственного носа или чужого затылка. Пустыня меняет человека. Наполовину это даже не человек, а животное, или если так угодно – робот, или все тот же человек с обостренным восприятием мира и расстроенной психикой? Союз нормальной во всех отношениях городской женщины и полудикого степного кочевника... будет очень коротким. Если вообще будет.
Принципы функционирования SRAM
Автор долго колебался – включать эту главу в книгу или нет. С одной стороны, для достижения грамотной работы с кэшем вдаваться в технические подробности устройства статической памяти совершенно необязательно, поскольку статическая память абсолютно прозрачна для программиста и конструктивные особенности ее реализации полностью маскируются кэш-контроллером. Но, в то же время, работать с "железкой", не имея никаких представлений о том, что находится у нее внутри – по меньшей мере невежественно, если не сказать "непрофессионально".
В конечном счете, небольшой ликбез никогда не помешает. Эта, весьма скромная по объему, глава ### статья, конечно же, не раскроет всех секретов статической памяти, но, по крайней мере, объяснит, что это такое и почему оно работает именно так, а не иначе.
Pro et contra целесообразности оптимизации
Это в наше-то время говорить об оптимизации программ? Бросьте! Не лучше ли сосредоточиться на изучении классов MFC или технологии .NET? Современные компьютеры так мощны, что даже Windows XP оказывается бессильна затормозить их!
Нынешние программисты к оптимизации относятся более чем скептически. Позволю себе привести несколько типичных высказываний:
"…я применяю относительно медленный и жадный до памяти язык, Perl, поскольку на нем я фантастически продуктивен. В наше время быстрых процессоров и огромной памяти эффективность – другой зверь. Большую часть времени я ограничен вводом/выводом и не могу читать данные с диска или из сети так быстро, чтобы нагрузить процессор. Раньше, когда контекст был другим, я писал очень быстрые и маленькие программы на C. Это было важно. Теперь же важнее быстро писать, поскольку оптимизация может привести к столь малому росту быстродействия, что он просто не заметен" говорит Robert White;
"…а стоит ли тратить усилия на оптимизацию и чего этим можно достичь? Дело в том, что чем сильнее вы будете адаптировать вашу программу к заданной архитектуре, тем, с одной стороны, вы достигнете лучших результатов, а, с другой стороны, ваша программа не будет хорошо работать на других платформах. Более того, "глубокая" оптимизация может потребовать значительных усилий. Все это требует от пользователя точного понимания чего он хочет добиться и какой ценой" пишет в своей книге "Оптимизация программ под архитектуру CONVEX C" М. П. Крутиков;
"Честно говоря, я сам большой любитель "вылизывания" кода с целью минимизации используемой памяти и повышения быстродействия программ. Наверное, это рудименты времен работы на ЭВМ с оперативной памятью в 32 Кбайт. С тем большей уверенностью я отношу "эффективность" лишь на четвертое место в критериях качества программ" признается Алексей Малинин – автор цикла статей по программированию на Visual Basic в журнале "Компьютер Пресс".
С приведенными выше тезисами, действительно, невозможно не согласиться. Тем не менее, не стоит бросаться и в другую крайность. Начертавший на своем знамени лозунг "на эффективность – плевать" добьется только того, что плевать (причем дружно) станут не в эффективность, а в него самого. Не стоит переоценивать аппаратные мощности! И сегодня существуют задачи, которым не хватает производительности даже самых современных процессоров. Взять хотя бы моделирование различных физических процессов реального мира, обработку видео-, аудио- и графических изображений, распознавание текста… Да что угодно, вплоть до элементарного сжатия данных архиватором a la Super Win Zip!
Да, мощности процессоров растут, но ведь параллельно с этим растут и требования к ним. Если раньше считалось нормальным, поставив программу на выполнение, уйти пить пиво, то сегодняшний пользователь хочет, чтобы все операции выполнялись мгновенно, ну если не мгновенно, то с задержкой не превышающей нескольких минут. Не стоят на месте и объемы обрабатываемых данных. Признайтесь, доводилось ли вам находить на своем диске файл размером в сотню-другую мегабайт? А ведь буквально вчера емкость целого жесткого диска была на порядок меньше!!!
Цель – определяет средства. Вот из этого, на протяжении всей книги, мы и будем исходить. Ко всем оптимизирующим алгоритмам будут предъявляется следующие жесткие требования:
а) оптимизация должна быть максимально машинно-независимой и переносимой на другие платформы (операционные системы) без дополнительных затрат и существенных потерь эффективности.
То есть никаких ассемблерных вставок! Мы должны оставаться исключительно в рамках целевого языка, причем, желательно использовать только стандартные средства, и любой ценой избегать специфичных расширений, имеющихся только в одной конкретной версии компилятора;
б) оптимизация не должна увеличивать трудоемкость разработки (в т.ч. и тестирования) приложения более чем на 10%-15%, а в идеале, все критические алгоритмы желательно реализовать в виде отдельной библиотеки, использование которой не увеличивает трудоемкости разработки вообще;
с) оптимизирующий алгоритм должен давать выигрыш не менее чем на 20%-25% в скорости выполнения.
Приемы оптимизации, дающие выигрыш менее 20% в настоящей книге не рассматриваются вообще, т.к. в данном случае "овчинка выделки не стоит". Напротив, основной интерес представляют алгоритмы, увеличивающие производительность от двух до десяти (а то и более!) раз и при этом не требующие от программиста сколь ни будь значительных усилий. И такие алгоритмы, пускай это покажется удивительным, в природе все-таки есть!
d) оптимизация должна допускать безболезненное внесение изменений. Достаточно многие техники оптимизации "умерщвляют" программу, поскольку даже незначительная модификация оптимизированного кода срубает всю оптимизацию на корню. И пускай все переменные аккуратно распределены по регистрам, пускай тщательно распараллелен микрокод и задействованы все функциональные устройства процессора, пускай скорость работы программы не увеличить и на такт, а ее размер не сократить и на байт! Все это не в силах компенсировать утрату гибкости и жизнеспособности программы. Поэтому, мы будем говорить о тех, и только тех приемах оптимизации, которые безболезненно переносят даже кардинальную перестройку структуры программы. Во всяком случае, грамотную перестройку. (Понятное дело, что кривые руки угробят что угодно – против лома нет приема).
Согласитесь, что такая постановка вопроса очень многое меняет. Теперь никто не сможет заявить, что, дескать, лучше прикупить более мощный процессор, чем тратить усилия на оптимизацию. Ключевой момент предлагаемой концепции состоит в том, что никаких усилий на оптимизацию тратить как раз не надо. Ну… почти не надо, – как минимум вам придется прочесть эту книжку, а это какие – ни какие, а все-таки усилия. Другой вопрос, что данная книга предлагает более или менее универсальные и вполне законченные решения, не требующие индивидуальной подгонки под каждую решаемую задачу.
Это одна из тех редких книг, если вообще не уникальная книга, которая описывает переносимую оптимизацию на системном уровне и при этом ухитряется не прибегать к ассемблеру.
Все остальные книги подобного рода, требуют свободного владения ассемблером от читателя. Впрочем, совсем уж без ассемблера обойтись не удалось, особенно в частях, посвященных технике профилировки и алгоритмам машинной оптимизации. Тем не менее, весь код подробно комментирован и его без труда поймет даже прикладной программист, доселе даже не державший отладчика в руках. Ассемблер, кстати, – это довольно простая штука, но его легче показать, чем описать.
И в заключении позвольте привести еще одну цитату:
"Я программирую, чтобы решать проблемы, и обнаружил, что определенные мысли блокируют все остальные мысли и творческие цели, которые у меня есть.
Это – мысли об эффективности в то время, когда я пытаюсь решить проблему. Мне кажется, что гораздо логичнее концентрироваться полностью на проблеме, решить ее, а затем творчески запрограммировать, затем, если решение медленное (что затрудняет работу с ним), то..."
Gary Mason.
Проблема наведенные эффектов
Исправляя одни ошибки, мы всегда потенциально вносим другие и потому после любых, даже совсем незначительных модификаций кода программы, цикл профилировки следует повторять целиком.
Вот простой и очень типичный пример. Пусть в оптимизированной программе встретилась функция следующего вида:
ugly_func(int foo)
{
int a;
…
…
…
if (foo<1) return ERR_FOO_MUST_BE_POSITIVELY;
for(a=1; a <= foo; a++)
{
…
…
…
}
}
Листинг 10 Фрагмент кода, демонстрирующий ситуацию, в которой удаление лишнего кода может обернуться существенным и труднообъясним падением производительности
Очевидно, если попытаться передать функции ноль или отрицательное число, то цикл for_a не выполнится ни разу, а потому принудительная проверка значения аргумента (в тексте она выделена жирным шрифтом) бессмысленна! Конечно, при больших значениях foo накладные расходы на такую проверку относительно невелики, но в праве ли мы надеяться, что удаление этой строки по крайней мере не снизит скорость выполнения функции?
Постойте, это отнюдь не бредовый вопрос, относящийся к области теоретической абстракции! Очень может статься так, что удаление выделенной строки будет носить эффект прямо противоположный ожидаемому, и вместо того чтобы оптимизировать функцию, мы даже снизим скорость ее выполнения, причем, весьма значительно!
Как же такое может быть? Да очень просто! Если компилятор не выравнивает циклы в памяти (как например, MS VC), то с довольно высокой степенью вероятности мы рискуем нарваться на кэш-конфликт (см. "Часть II. Кэш"), облагаемый штрафным пенальти. А можем и не нарваться! Это уж как фишка ляжет. Быть может, эта абсолютно бессмысленная (и, заметьте, однократно
выполняемая) проверка аргументов как раз и спасала цикл от штрафных задержек, возникающих в каждой итерации.
Сказанное относится не только к удалению, но и вообще любой модификации кода, влекущий изменение его размеров.
В ходе оптимизации производительность программы может меняться самым причудливым образом, то повышаясь, то понижаясь без всяких видимых на то причин. Самое неприятное, что подавляющее большинство компиляторов не позволяют управлять выравниванием кода и, если цикл лег по неудачным с точки зрения процессора адресам, все, что нам остается – добавить в программу еще один кусок кода с таким расчетом, чтобы он вывел цикл из неблагоприятного состояния, либо же просто "перетасовать" код программы, подобрав самую удачную комбинацию.
"Идиотизм какой-то", – скажите вы и будете абсолютно правы. К счастью, тот же MS VC выравнивает адреса функций по адресам, кратным 0x20 (что соответствует размеру одной кэш-линейки на процессорах P6 и K6). Это исключает взаимное влияние функций друг на друга и ограничивает область тасования команд рамками всего "лишь" одной функции.
Тоже самое относится и к размеру обрабатываемых блоков данных, числу и типу переменных и т.д. Часто бывает так, что уменьшение количества потребляемой программой памяти приводит к конфликтам того или иного рода, в результате чего производительность естественно падает. Причем, при работе с глобальными и/или динамическими переменными мы уже не ограничивается рамками одной отдельно взятой функции, а косвенно воздействуем на всю программу целиком! (см. "Часть I. Конфликт DRAM банков").
Сформулируем три правила, которыми всегда следует руководствоваться при профилировке больших программ, особенно тех, что разрабатываются несколькими независимыми людьми. Представляете – в один "прекрасный" день вы обнаруживаете, что после последних внесенных вами "усовершенствований" производительность вверенного вам фрагмента неожиданно падает… Но, чтобы вы не делали, пусть даже выполнили "откат" к прежней версии, вернуть производительность на место вам никак не удавалось. А на завтра она вдруг – без всяких видимых причин! – восстанавливалась до прежнего уровня сама.Да, правильно, причина в том, что ваш коллега чуть-чуть изменил свой модуль, а это "рикошетом" ударило по вам!
Итак, обещанные правила:
Первое: никогда – никогда не оптимизируйте программу "вслепую", полагаясь на "здравый смысл" и интуицию;
Второе: каждое внесенное изменение проверяйте на "вшивость" профилировщиком и, если производительность неожиданного упадает, вместо того чтобы увеличиться, незамедлительно устаивайте серьезные разборки: "кто виноват" и "чья тут собака порылась", анализируя весь, а не только свой собственный код;
Третье: после завершения оптимизации локального фрагмента программы, выполните контрольную профилировку всей программы целиком на предмет обнаружения новых "горячих" точек, появившихся в самых неожиданных местах.
Проблема второго прохода
Для достижения приемлемой точности измерений профилируемое приложение следует прогнать по крайней мере 9– 12 раз (см. "Непостоянства времени выполнения. Обработка результатов измерений"), причем каждый прогон должен осуществляться в идентичных условиях окружения. Увы! Без написания полноценного эмулятора всей системы это требование практически невыполнимо. Дисковый кэш, сверхоперативная память обоих уровней, буфера физических страниц и история переходов чрезвычайно затрудняют профилировку программ, поскольку при повторных прогонах время ее выполнения значительно сокращается.
Если мы профилируем многократно выполняемый цикл, то этим обстоятельством можно и пренебречь, поскольку время загрузка данных и/или кода в кэш практически не сказывается на общем времени выполнения цикла. К сожалению, так бывает далеко не всегда (такой случай как раз и был разобран в главе "Цели и задачи профилировки. Информация о пенальти").
Да и можем же мы наконец захотеть оптимизировать именно инициализацию приложения?! Пускай, она выполняется всего лишь один раз за сеанс, но какому пользователю приятно, если запуск вашей программы растягивается на минуты и то и десятки минут? Конечно, можно просто перезагрузить систему, но… сколько же тогда профилировка займет времени!
Хорошо. Очистить кэш данных – это вообще раз плюнуть. Достаточно считать очень большой блок памяти, намного превышающий его (кэша) емкость. Не лишнем будет и записать большой блок для выгрузки всех буферов записи (см. "Часть II. Кэш"). Это же, кстати, очистит и TLB (Translate Look aside Buffer) – буфер, хранящий атрибуты страниц памяти для быстрого обращения к ним (см. "предвыборка?"). Аналогичным образом очищается и кэш/TLB кода. Достаточно сгенерировать очень большую функцию, имеющую размер порядка 1 – 4 Мб, и при этом ничего не делающую (для определенности забьем ее NOP'ами – машинными командами "нет операции"). Всем этим мы уменьшим пагубное влияние всех, перечисленных выше эффектов, хотя и не устраним его полностью.
Увы! В этом мире есть вещи, не подвластные ни прямому, ни косвенному контролю (во всяком случае на прикладном уровне).
С другой стороны, если мы оптимизируем одну, отдельно взятую функцию, (для определенности остановимся на функции реверса строк), то как раз таки ее первый прогон нам ничего не даст, поскольку в данном случае основным фактором, определяющим производительность, окажется не эффективность кода/алгоритма самой функции, а накладные расходы на загрузку машинных инструкций в кэш, выделение и проецирование страниц операционной системой, загрузку обрабатываемых функцией данных в сверхоперативную память… В реальной же программе эти накладные расходы как правило уже устранены (даже если эта функция вызывается однократно).
Давайте проведем следующий эксперимент. Возьмем следующую функцию и десять раз подряд запустим ее на выполнение, замеряя время каждого прогона.
#define a (int *)((int)p + x)
A_BEGIN(0)
#define b (int *)((int)p + BLOCK_SIZE - x - sizeof(int))
for (x = 0; x < BLOCK_SIZE/2; x+=sizeof(int))
{
#ifdef __OVER_BRANCH__
if (x & 1)
#endif
*a = *a^*b; *b = *b^*a; *a = *a^*b;
}
A_END(0)
Листинг 9 Пример функции, однократно обращающийся к каждой загруженной в кэш ячейке
Для блоков памяти, полностью умещающихся в кэш-памяти первого уровня, на P-III 733/133/100/I815EP мы получим следующий ряд замеров:
__OVER_BRANCH__ not define __OVER_BRANCH__ is define
68586 63788
17629 18507
17573 18488
17573 18488
17573 18488
17573 18488
17573 18488
17573 18488
Обратите внимание: время выполнения первого прогона функции (не путать с первой итерации цикла!) практически вчетверо превосходит все последующие! Причем, результаты замеров непредсказуемым образом колеблются от 62.190 до 91.873 тактов, что соответствует погрешности ~50%.
Означает ли это, что если данный цикл в реальной программе исполняется всего один раз, то оптимизировать его бессмысленно? Конечно же нет! Давайте, для примера избавимся от этого чудачества с XOR и как нормальные люди обменяем два элемента массива через временную переменную. Оказывается, это сократит время первого прогона до 47.603 – 65.577 тактов, т.е. увеличит эффективность его выполнения на 20% – 40%!
Тем не менее, устойчивая повторяемость результатов начинается лишь с третьего прогона! Почему так медленно выполняется первый прогон – это понятно (загрузка данных в кэш и все такое), но вот что не дает второму показать себя во всю мощь? Оказывается – ветвления. За первый прогон алгоритм динамического предсказания ветвлений еще не накопил достаточное количество информации и потому во втором прогоне еще давал ошибки, но начиная с третьего наконец-то "въехал" в ситуацию и понял, что от него ходят.
Убедиться, что виноваты именно ветвления, а ни кто ни будь другой, позволяет следующий эксперимент: давайте определим __OVER_BRANCH__ и посмотрим как это скажется на результат. Ага! Разница между вторым и третьим проходом сократилась с 0,3% до 0,1%. Естественно, будь наш алгоритм малость поразлапистее (в смысле – "содержи побольше ветвлений"), и всех трех прогонов могло бы не хватить для накопления надежного статистического результата. С другой стороны, погрешность, вносимая переходами, крайне невелика и потому ей можно пренебречь. Кстати, обратите внимание, что постоянство времени выполнения функции на всех последних проходах соблюдается с точностью до одного такта!
Таким образом, при профилировании многократно выполняющихся функций, результаты первых двух – трех прогонов стоит вообще откинуть, и категорически не следует их арифметически усреднять.
Напротив, при профилировании функций, исполняющихся в реальной программе всего один раз, следует обращать внимание лишь на время первого прогона и отбрасывать все остальные, причем, при последующих запусках программы необходимо каким либо образом очистить все кэши и все буфера, искажающие реальную производительность.
Проблемы оптимизации программ на отдельно взятой машине
Большинство программистов, особенно их тех, что пасутся на вольных хлебах, имеют в своем распоряжении одну, ну максимум две машины, на которой и осуществляются все стадии создания программы: от проектирования до отладки и оптимизации. Между тем, как уже успел убедиться читатель "что русскому хорошо, то немцу – смерть". Код, оптимальный для одной платформы, может оказаться совсем неоптимальным для другой. Планирование потоков данных (см. одноименную главу) – яркое тому подтверждение. Ну вспомните: особенности реализации предвыборки данных в чипсете VIA KT133 приводят к резкому падению производительности при параллельной обработке нескольких близко расположенных потоков. Об этом малоприятном факте умалчивает документация, он не может быть предвычислен логически, – обнаружить его можно лишь экспериментально.
Совершенно недопустимо профилировать программу на одной-единственной машине, – это не позволит выявить все "узкие" места алгоритма. Следует, как минимум, охватить три-четыре типовые конфигурации, обращая внимания не только на модели процессоров, но и чипсетов. Этим вы более или менее застрахуете себя от "сюрпризов", подобных уже описанным странностям чипсета VIA KT 133.
Сложнее найти компромисс, наилучшим образом "вписывающийся" во все платформы.
Проблемы тестирования оперативной памяти
Разгон памяти – весьма радикальное средство увеличения производительности, но и чрезвычайно требовательное к качеству модулей памяти. Впрочем, некачественные модули могут сбоить даже в штатном режиме безо всякого разгона. Последствия таких ошибок весьма разнообразны: от аварийного завершения приложения до потери и/или искажения обрабатываемых данных. Судя по всему, приобретение "битой" памяти – отнюдь не редкость и со сбоями памяти народ сталкивается достаточно регулярно. Забавно, но подавляющее большинство разработчиков программного обеспечения начисто игнорируют эту проблему, заявляя, что всякое приложение вправе требовать для своей работы исправного "железа". Теоретически оно, может быть и так, но на практике факт исправности железа предстоит еще подтвердить. Причем, популярные диагностические утилиты (такие, например, как Check It) для этой цели абсолютно не пригодны. За исключением совсем уж клинических случаев, тест проходит без малейших помарок, но стоит запустить тот же Word или Quake, как система мгновенно виснет. Меняем модуль память – все работает на ура. Выходит, виновата все же память? Тогда почему это не обнаружил CheckIt?!
Причина в том, что далеко не всякая неисправность чипа памяти приводит к его немедленному отказу. Чаще всего дефект проявляется лишь при определенном стечении ряда обстоятельств. Тяжеловесное приложение, гоняющее память "и в хвост, и в гриву", имеет все шансы за короткое время "подобрать" нужную комбинацию, провоцирующую сбой. Популярные диагностические программы, напротив, тестируют весьма ограниченный спектр режимов в весьма щадящих условиях. Соответственно, и вероятность обнаружить ошибку в последнем случае значительно ниже.
Выход? – Разрабатывать собственную тестирующую программу. Во-первых, необходимо учитывать, что вероятность сбоя тесно связана с температурой кристалла. Чем выше температура – тем вероятнее сбой. А температура в свою очередь зависит от интенсивности работы памяти. При линейном чтении ячеек, микросхема памяти за счет пакетного режима успевает несколько приостыть, поддерживая внутри себя умеренную температуру.
Действительно, при запросе одной ячейки, вся DRAM-страница читается целиком, сохраняясь во внутренних буферах и до тех пор, пока не будет запрошена следующая страница этого же банка, никаких обращений к ядру памяти не происходит!
Поэтому, прежде чем приступать к реальному тестированию, память необходимо как следует прогреть, читая ее с шагом, равным длине DRAM-банка. Это заставит ядро данного банка работать максимально интенсивно, на каждом шаге выполняя процедуру чтения и восстанавливающей записи данных. Не стоит тестировать несколько банков одновременно. Во-первых, это несколько снизит температуру "накала" каждого из них, а, во-вторых, перепад температур внутри кристалла увеличивает вероятность обнаружения сбоя. (Вообще-то, микросхеме при этом приходится по-настоящему туго, но она обязана выдержать такой режим работы, в противном случае, ее место – на свалке).
Ага, модуль памяти нагрелся так, что не удержишься рукой. Самое время приступать к настоящим тестам. Заполняем DRAM-страницу контрольной последовательностью чисел (далее по тексту – шаблоном), переключаем страницу, чтобы гарантированно обновить ячейки памяти (в противном случае микросхема может возвратить содержимое своих буферов, не обращаясь к матрице памяти). Вновь переключаем страницу назад и проверяем, что мы записали. Это может выглядеть приблизительно так:
for (a=0; a < DRAM_BANK_SIZE; a += DRAM_PAGE_SIZE)
{
WriteTemplate(a); // записываем шаблон
x = (DRAM_BANK_SIZE-a); // переключаем DRAM-страницу
CompareTemplate(a); // проверяем, что мы записали
}
Листинг 46 Упрощенный пример реализации функции тестирования памяти
Причем, к шаблону предъявляются весьма жесткие требования. Во-первых, он должен тестировать каждый бит ячейки, причем на оба значения – единицу и нуль, поскольку, "битые" ячейки матрицы могут давать либо "всегда ноль", либо "всегда единица". Во-вторых, крайне желаться, чтобы во всем восьмерном слове соседние биты имели противоположные значения.
Такая комбинация создает наибольший уровень помех и тем самым провоцирует систему на ошибку. Третье, шаблон должен обеспечивать выявление ошибок адресации, – т.е. микросхема возвратила содержание ячейки не той строки и/или столбца.
Поскольку, все эти требования взаимоисключающие, для тестирования потребуется несколько шаблонов. Только не забывайте время от времени выполнять "холостое" чтение для поддержания температуры микросхемы на максимально достижимом уровне, иначе эффективность теста начнет падать.
Остается обсудить лишь последовательность перебора станиц. Первое, что приходит на ум, тривиальный последовательный перебор, затем – хаотичное обращения к страницам по случайному шаблону. Достаточно ли этого для выявления всех типов ошибок? К сожалению, нет. Многие (если не все) современные контроллеры памяти самостоятельно определяют предпочтительный порядок обработки запросов. Возьмем, например, листинг рассмотренный выше. Контролер, проанализировав очередь запросов, видит, что двойного переключения страниц можно избежать, если… не выполнять повторное чтение из матрицы памяти, а возвратить процессору содержимое буфера! Похоже, есть только один путь обхитрить контроллер, – проверять ячейки не сразу после записи, а спустя некоторое время, когда внутренние буфера контроллера будут гарантированно перекрыты последующими запросами. Это же, кстати, позволяет выявить ошибки регенерации, – когда из-за каких-то дефектов заряд с ячейки матрицы стекает раньше, чем ее успевают регенерировать.
И в заключении – о ECC (Error Checking and Correction – Выявление и Исправление Ошибок). Теоретически система с поддержкой ECC (а таких на сегодняшний день большинство) должна уметь распознавать одиночные сбои памяти и, если не исправлять, то, по крайней мере, останавливать систему в случае обнаружения двойного сбоя. Ну, насчет испр
Рекомендуемые ссылки
http://www.gvu.gatech.edu/gvu/people/randy.carpenter/folklore/
Программирование на ассемблере как особый род творчества
Компьютер уже давно перестал быть машиной для небольшой горстки Избранных и с каждым днем он все стремительнее и стремительнее превращается в… пылесос. Ну, или что-то очень на него похожее. Современные программисты, абстрагировавшись от "железа" и даже от самих вычислительных алгоритмов, видят перед собой лишь мышь да визуальную панель с компонентами. Написать программу стало так же легко, как сварить пакетный суп. Конечно, свои положительные моменты в этом есть, но… существует определенная категория людей, для которых жизнь – ни на секунду не прекращающийся поиск и преодоление сложностей (ни слова по гамак и ласты!). Если задуматься: какую практическую ценность несет в себе, ну скажем, покорение горных вершин? Ведь гораздо комфортнее и куда с меньшим риском к ним можно добраться и на вертолете…
Увы! Чем легче достается, – тем меньше удовлетворения оно приносит. Визуальное программирование слишком просто, чтобы быть по настоящему интересным. С другой стороны, чем выше уровень языка, тем больше приходится соблюдать предписаний, и тем меньше остается возможности для самовыражения. А Художники как раз и отличаются от окружающих тем, что в каждой работе передают свое видение мира, частицу своего "Я".
Интерес к ассемблеру, часто доходящий до фанатизма, как раз и объясняется тем, что ассемблер – лучшее средство "пощупать" железо компьютера; это превосходная арена для интеллектуальной борьбы, и, наконец, – великолепный способ с пользой и интересом скоротать свободное от работы время.
Существует огромное множество ассемблерных головоломок – от "написать программу на байт короче, чем у соседа", до "создать самообучающуюся шахматную игру, занимающую не более двух килобайт". На ассемблере пишутся многие "демки", на нем же создаются "крякмисы" (в дословном переводе "взломай меня")… Никто не спорит, что все, перечисленное выше, можно реализовать и на языках высокого уровня, причем за несравнимо более короткое время при не сильно худшей эффективности. Да! Можно! Но… неинтересно. Мы, комсомольцы, видите ли, без ласт и гамака любить не можем…
Поэтому (и это очень важно!), если вы встретите человека, беззаветно преданного ассемблеру и презирающего языки высокого уровня, не спешите ломать пальцы о клавиатуру, переубеждая его в обратном. Девять из десяти – ассемблер любит он не за достоинства, а, напротив, за отсутствие таковых (если понимать под "достоинствами" удобства цивилизации). Один из десяти – он просто выпендривается и программирует на ассемблере, чтобы продемонстрировать окружающим свою крутость. Тогда тем более не стоит его переубеждать – с возрастом само рассосется.
Программная предвыборка в процессорах K6+ и P-III+
Поддержка программной предвыборки имеется как в K6 (и совместимом с ним микропроцессоре VIAC3), так и в P-III\P-4, однако, их реализации различны и к тому же несовместимы друг с другом. Это печальное обстоятельство существенно снижает популярность предвыборки, поскольку программистам приходится либо реализовывать использующие ее функции в двух вариантах один для Intel, другой – для AMD (VIA), либо ограничивать аудиторию пользователей каким-то одним процессором. И то, и другое влечет за собой большие издержки, зачастую не компенсируемые увеличением производительности приложения.
Появление процессора AMD Athlon, поддерживающего "дуальный" набор команд предвыборки, обещает исправить сложившуюся ситуацию, хотя на этом пути еще много нерешенных проблем и программному управлению кэшированием ох как не просто отвоевать свой кусок места под солнцем.
Ввиду прекращения производства K6 и его неизбежного вытеснения с рынка, команды предвыборки из набора 3D Now! в настоящей главе рассматриваются лишь кратко, а основное внимание уделяется командам предвыборки, входящим в состав набора MMX-команд, который поддерживается практически всеми современными процессорами.
Поэтому, к предвыборке целесообразно прибегать лишь в действительно крайних случаях, когда никакими другими путями обеспечить требуемое быстродействие уже не удается.
Программное непостоянство
В многозадачной среде, коей и является популярнейшая на сегодняшний день операционная система Windows, никакая программа не владеет всеми ресурсами системы единолично и вынуждена делить их с остальными задачами. А это значит, что скорость выполнения профилируемой программы не постоянна и находится в тесной зависимости от "окружающей среды". На практике разброс результатов измерений может достигать 10% –15%, а то и больше, особенно если параллельно с профилировкой исполняются интенсивно нагружающие систему задачи.
Тем не менее, особой проблемы в этом нет, – достаточно лишь в каждом сеансе профилировки делать несколько контрольных прогонов и затем… нет, не усреднять, а выбирать замер с наименьшим временем выполнения. Мотив такой: измерения производительности – это не совсем обычные инструментальные измерения и типовые правила метрологии здесь неуместны. Процессор никогда не ошибается и каждый полученный результат точен. Другое дело, что он в той или иной степени искажен побочными эффектами, но! никакие побочные эффекты никогда не приводят к тому, чтобы программа начинает исполняться быстрее, нежели она исполняется в действительности, а потому, прогон с минимальным временем исполнения и представляет собой измерение в минимальной степени испорченное побочными эффектами.
Кстати, во многих руководствах утверждается, что перед профилировкой целесообразно выходить из сети ("что бы машина не принимала пакеты"), завершать все-все приложения, кроме самого профилировщика и вообще лучше даже "на всякий случай" перегрузиться. Все это чистейшей воды гон! Автор частенько отлаживал программы параллельно с работой в Word'e, приемом корреспонденции, скачкой нескольких файлов из Интернет и – точностью профилировки всегда оставалась удовлетворительной! Конечно, без особой нужды не стоит так рисковать, и параллельно работающие приложения перед началом профилировки, действительно, лучше завершить, но не следует доводить ситуацию до абсурда, и пытаться обеспечить полную "стерильность" своей машине.
Протокол MESI
Под загадочной аббревиатурой MESI, частенько встречающийся в отечественной и зарубежной литературе, скрывается ни что иное, как первые буквы четырех статусов кэш-линейки Modified Exclusive Shared Invalid (Модифицированная Девственная Скоммунизденая Инвалидная).
Но что каждый из этих статусов обозначает? Вот это мы сейчас и рассмотрим! Итак…
Статус "Modified" автоматически присваивается кэш-строкам при их модификации. Строка с таким атрибутом не может быть просто выброшена из кэша и при ее вытеснении обязательно должна выгружаться в кэш память более высокой иерархии или же основную память;
Статус "Exclusive" автоматически присваивается кэш-строкам при их загрузке из кэша более высокой иерархии или основной оперативной памяти. Модификация строки с атрибутом Exclusive влечет его автоматическую смену на атрибут Modified.
Строка с атрибутом Exclusive при ее вытеснении из кэша в зависимости от архитектурных особенностей системы либо просто уничтожается (inclusive - кэш), либо обменивается своим содержимым с одной из строк кэш-памяти более высокой иерархии (exclusive – кэш). см. так же. "Двухуровневая организация кэша"
Статус "Shared" присваивается кэш-строкам, потенциально присутствующим в кэш-памяти других процессоров (если это многопроцессорная система). Помимо этого, атрибут Shared указывает еще и на то, что строка когерентна содержимому соответствующих ей ячеек основной памяти. Поскольку, многопроцессорные системы далеко выходят за рамки нашего разговора, отложим этот вопрос до специального тома книги.
(Примечание: в AMD Athlon добавился новый статус "Owner" – "Владелец", и сам протокол стал записываться так: MOESI. Подробнее об этом будет так же рассказано в томе, посвященном многопроцессорным архитектурным).
Статус "Invalid" строка отсутствует в кэше и должна быть загружена из кэш памяти более высокой иерархии или же основной памяти.
Кэш данных первого уровня и кэш второго уровня Pentium- и AMD K6\Athlon процессоров поддерживает все четыре статуса, а кэш кода – только два из них Shared и Invalid. Остальные не поддерживаются по той простой причине, что кодовый кэш не допускает модификации своих линеек. А как же в этом случае работает самомодифицирующий код? – удивится иной читатель. А кто вам сказал, что он вообще работает? – возражу я. Независимо от того, присутствует ли модифицируемая ячейка в кодовом кэше или нет, инструкция записи не может непосредственно изменить ее содержимое, и она помещается в кэш первого (второго) уровня или основную оперативную память. Несмотря на то, что процессор все-таки отслеживает эти ситуации и обновляет соответствующие строки кодового кэша, самомодифицирующегося кода по возможности следует избегать, поскольку: во-первых, при обновлении строк гибнет вся преддекодированная информация, а, во-вторых, процессору приходится очищать конвейер и вновь начинать его заполнять сначала.
Причем, под самомодифицирующимся кодом в современных системах понимается не только истинно самомодифицирующийся код в его каноническом понимании, но и вообще всякая запись в область памяти, находящуюся в кодовом кэше. То есть, смесь кода и данных, которая так часто встречается в "ручных" ассемблерных программах, будет исполняться не скорее асфальтового катка, хотя формально она и не изменяет машинный код (но процессор-то об этом не знает!).
|
Статус |
Modified |
Exclusive |
Shared |
Invalid |
|
эта кэш линия действительна? |
да |
да |
да |
нет |
|
копия в памяти действительна? |
устарела |
действительна |
действительна |
этой строке вообще не соответствует никакая память |
|
содержится ли копия этой строки в других процессорах? |
нет |
нет |
может быть |
может быть |
|
запись в эту линию осуществляется… |
только в эту строку, без обращения к шине |
только в эту строку, без обращения к шине |
сквозной записью в память с аннулированием строки в кэшах остальных процессоров |
непосредственно через шину |
